Calculating Signal-to-Noise Ratio Using DFT
This article addresses the use of the Signal-to-Noise ratio (SNR) in a filter function and its application in a Low-Pass Filter.
September 22, 2020
Read through the articles related to the Discrete Fourier Transform (DFT) for time series.
This article addresses the use of the Signal-to-Noise ratio (SNR) in a filter function and its application in a Low-Pass Filter.
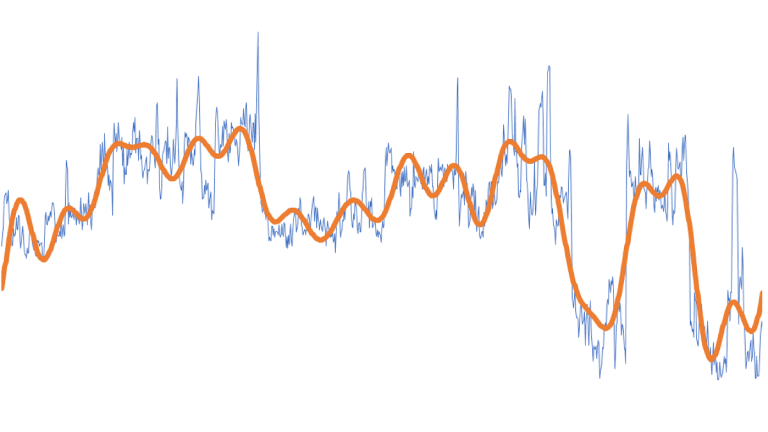
This issue addresses how to use Fourier Transform to filter a data signal using only K frequency components with the highest amplitudes.
This issue focuses on using the DFT components to represent the input data set as the sum of the trigonometric sine-cosine functions.
In this entry, we examine the Discrete Fourier Transform (DFT) and its inverse, as well as data filtering using DFT outputs.
© 2025 Spider Financial Corp | Terms & Conditions | Disclaimer | Privacy Policy | Trademarks & Copyrights
