Manejo de valores faltantes
Este número es el primero de una serie de artículos que exploran el aspecto de preparación de datos del análisis de series de tiempo. A menudo los analistas pasan por alto la preparación de datos, pero creemos que es una fase vital que ejerce una vasta influencia en el análisis general y el proceso de modelado. La gran mayoría de las series temporales y las teorías econométricas suponen que las series temporales de entrada son estacionarias y homogéneas, con observaciones y valores igualmente espaciados que están presentes y reales. En la práctica, a menudo manejamos muestras con valores faltantes, observaciones espaciadas de manera desigual, posibles valores atípicos, dependencia de media / varianza, rangos de valores restringidos y otros fenómenos. El objetivo de esta serie de artículos es abordar cada uno de estos problemas e introducir métodos prácticos para superarlos.
En este tema, partimos de los supuestos de muestreo de la serie temporal: espaciamiento igual e integridad. Luego consideramos una serie temporal con valores faltantes y discutimos cómo representarlos en Excel, con la ayuda del procesamiento NumXL. Finalmente, miramos series temporales desigualmente espaciadas, cómo llegan a existir, cómo se relacionan con el escenario de valores perdidos y qué hacer con ellos.
Muestreo en series de tiempo
La situación común (perfecta) para una muestra de series temporales es aquella que tiene observaciones igualmente espaciadas y valores presentes para todos los puntos. Esto se debe a que las observaciones se hacen deliberadamente enintervalos uniformes (proceso continuo), o porque el proceso sólo genera salidasa tal intervalo de tiempo (proceso discreto).
Además, la unidad de tiempo para un período de muestreo (es decir, paso) entre dos observaciones consecutivas puede ser absoluta (por ejemplo, diaria, semanal, mensual o anual) o basarse en un calendario de vacaciones (es decir, ajustado para fines de semana y días festivos). Por ejemplo, una serie cronológica financiera diaria de precios de cierre de acciones de IBM se basa en el calendario de días feriados NYSE, por lo que cada observación se toma en un día laboral o de negociación de la NYSE (apertura / cierre).
Con respecto al modelado y pronóstico de series de tiempo, no es importante si usamos el tiempo absoluto o si nos ajustamos para fines de semana y días festivos. Lo importante es cómo interpretamos las fechas fuera de la muestra, ya que también se basan en el mismo método de muestreo.
A continuación, vamos a examinar algunos casos en los que la serie de tiempo de entrada no es tan perfecto.
Issue 1: Valores faltantes
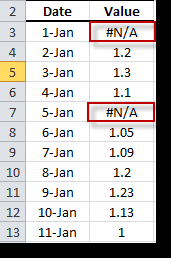
En algunas situaciones, una o más fechas de observación producen valores inválidos o faltantes. Estos valores se designan como “no-valores”, o NaN para abreviar. En Excel, NaN se identifica con la representación especial “#N/A”, y pocas funciones incorporadas pueden ser utilizadas para detectar (por ejemplo, NA (), ISNA (.), IFERROR (.), Etc.) o ignorarlas (Por ejemplo, MIN (.), MAX (.)), Y otras funciones no son de apoyo.
En el análisis de series de tiempo, a menudo encontramos fenómenos de valores perdidos, ya sea en la serie de tiempo cruda original o como resultado de un operador de series de tiempo (por ejemplo, lag, diferenciación, etc.).
NumXL tine dos simples reglas:
- Los valores faltantes en el comienzo o al final de la serie de tiempo son simplemente ignoradas. NumXL truncará la serie de tiempo de entrada para comenzar desde el primer valor no faltante y terminará con el último valor no faltante.
- Los valores intermedios que faltan se consideran fallas graves en la serie de tiempo de entrada, y NumXL no puede procesarlos.
Estas reglas plantean la pregunta: Cómo manejamos los valores intermedios faltantes?
Se han propuesto muchas técnicas para manejar series de tiempo con datos faltantes, pero podemos resumir estas propuestas con dos principios:ignorar e interpolar.
IGNORAR
La solución ignorar simplemente descarta el valor faltante de la serie de tiempo. Puede utilizar la función de NumXL RMNA (.) Función para este fin. Sin embargo, debe abordar esta solución con cautela, ya que altera el muestreo de la serie de tiempo en sí.
INTERPOLAR
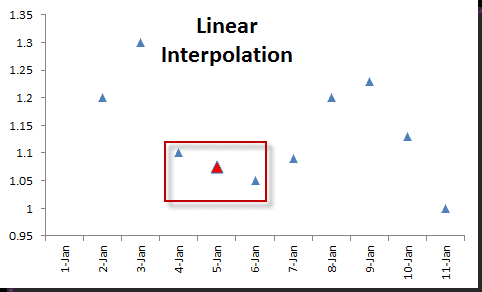
El método de interpolación sustituye los valores faltantes por valores interpolados. Existen varios algoritmos de interpolación en Excel: lineal, polinomial, suavizado, spline, filtrado, etc.
La interpolación en Excel no cambia la frecuencia del muestreo, pero puede afectar la dinámica percibida del proceso subyacente si se utiliza para varios puntos de la serie temporal.
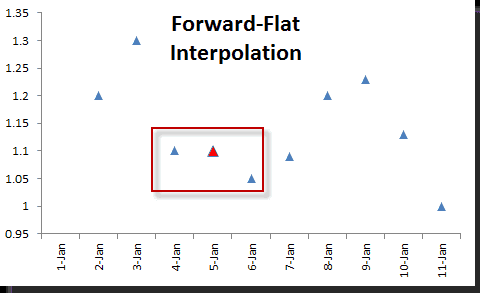
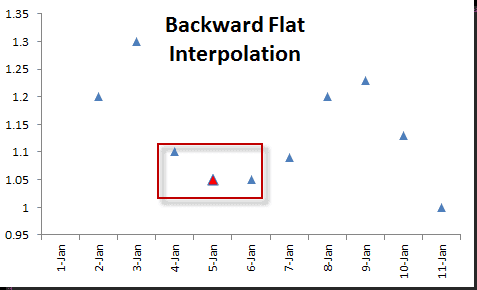
NumXL viene con una función de interpolación en ExcelINTERPOLACION– la que asiste cuatro (4) differentes Interpolaciones en Excel algoritmos:
Hacia adelante & Interpolación plana hacia atrás en Excel
Lineal & Interpolación de spline cúbico en Excel
Issue 2: Series temporales desigualmente espaciadas
Las series temporales desigualmente espaciadas son comunes en muchas aplicaciones de la vida real cuando las mediciones están restringidas por condiciones prácticas.La irregularidad de las observaciones puede tener varias razones fundamentales. Primero, cualquier proceso de recolección impulsado por eventos (en el cual se obtiene la observación cuando ocurre algún evento) es inherentemente irregular.En segundo lugar, en aplicaciones tales como redes de sensores o cualquier infraestructura de supervisión distribuida, la recopilación de datos se distribuye y los agentes de recopilación no pueden sincronizarse fácilmente entre sí. Además, los intervalos de muestreo y las políticas pueden ser diferentes. Finalmente, las mediciones no se pueden realizar regularmente o pueden ser interrumpidas debido a algunos eventos (previstos o no).
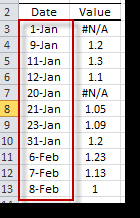
A diferencia del caso de serie temporal de iguales intervalos, las observaciones intermedias con valores faltantes pueden ser eliminadas con seguridad de la serie original sin ninguna pérdida de información, y, obviamente, la serie resultante también está espaciada de manera irregular.
Se han propuesto muchas técnicas para manejar series de tiempo con datos faltantes, los cuales en el límite pueden ser vistos como muestras irregulares.
En la práctica del análisis de datos, la irregularidad es una característica reconocida de los datos, y los profesionales la tratan heurísticamente.
Solution 1: Convertir a series de tiempo igualmente espaciadas
- IGNORA: IGNORAR la irregularidad en los tiempos y tratar los datos como si fueran regulares.
- REMUESTREO: REMUESTREO utilizando una tasa de muestreo menor.
La reducción simplifica el problema a uno que ya ha sido analizado a fondo
y para el cual existen muchos enfoques disponibles.
Nota: Para una serie temporal de precios, el muestreo descendente requiere tomar la última observación en el nuevo período de muestreo. Para el retorno del registro de esta estrategia, el retorno de re-muestreo es el retorno acumulado de todos los períodos en los períodos de muestra originales./p>
- INTERPOLACION: Interpola los valores intermedios faltantes y convierte la serie a una con tiempos de muestreo igualmente espaciados. Mientras esto es una heurística razonable para tratar con valores faltantes, el proceso de Interpolación in Excel típicamente resulta en un sesgo significativo (por ejemplo, suavizado de los datos) que cambia la dinámica del proceso, por lo que estos modelos no pueden aplicarse si los datos están realmente espaciados de forma desigual.
- Suavizado de Kernel
- Puente Browniano: Varios autores han sugerido usar procesos continuos de difusión de tiempo para encontrar valores perdidos. En principio, para interpolar un valor faltante, asumimos un movimiento browniano entre los valores inmediatamente antes y después de las observaciones no faltantes.
A la fecha de este número, NumXL no admite el método de interpolación puente Browniano en Excel.
Solución II - Utiliza modelos de series de tiempo desigualmente espaciadas
Estos modelos son ligeramente más complejos que sus modelos homólogos igualmente espaciados, y muchos pueden ser vistos como una extensión de los modelos de series temporales igualmente espaciados.
Suponiendo que $Y(t)$ es una serie de tiempo con muestreo irregular, podemos descomponerla en:
$$Y(t)=a(t)+X(t)$$
Donde:
- $a(t)$ Es una función determinista que cambia lentamente (componente de tendencia)
- $X(t)$ Es un componente de ruido aleatorio
En general, uno puede solo observar $Y(t)$, nuestro primer objetivo es estimar el componente determinístico y our first goal is to estimate the deterministic component Y extraer el ruido aleatorio$ X(t)=Y(t)-a(t)$; nuestro segundo objetivo es encontrar un modelo probabilístico satisfactorio para el proceso $X(t)$
A partir de la fecha de este número, NumXL no admite modelos de series temporales desigualmente espaciados.