Suavizado Exponencial Simple de Brown
El suavizado simple exponencial es similar al promedio móvil ponderado (WMA) con la excepción de que el tamaño de la ventana es infinito y los factores de ponderación disminuyen exponencialmente.
$$Y_1=X_1$$ $$Y_2=(1-\alpha)Y_1+\alpha X_1=X_1$$ $$Y_3=(1-\alpha)Y_2+\alpha X_2=(1-\alpha)X_1+\alpha X_2$$ $$Y_4=(1-\alpha)Y_3+\alpha X_3=(1-\alpha)^2 X_1+\alpha (1-\alpha) X_2+\alpha X_3$$ $$Y_5=(1-\alpha)^3 X_1+\alpha (1-\alpha)^2 X_2+\alpha (1-\alpha) X_3 + \alpha X_4$$ $$Y_{T+1}=(1-\alpha)^T X_1+\alpha \sum_{i=1}^T (1-\alpha)^{T-i}X_{i+1}$$ $$\cdots$$ $$Y_{T+m}=Y_{T+1}$$
Dónde:
- $\alpha$ es el factor de suavizado ($0 \prec \alpha \prec 1$)
Cómo hemos visto en el WMA, el exponencial simple es adecuado para series de tiempo con una media estable, o al menos una media móvil muy lenta.
Ejemplo 1:
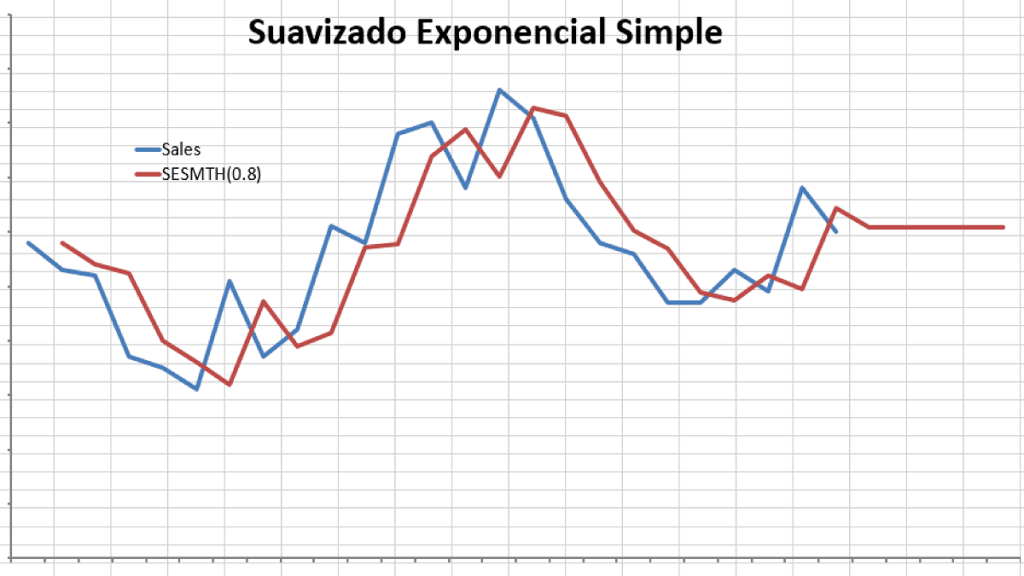
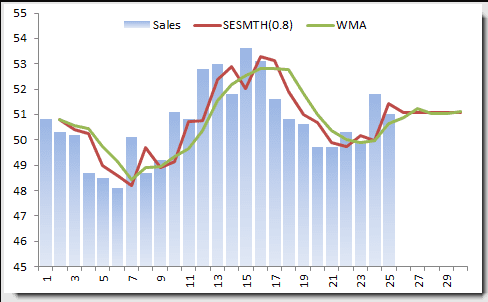
Vamos a usar los datos de ventas mensuales (como lo hicimos en el ejemplo de WMA).
En el ejemplo anterior, elegimos el factor de suavizado para que sea 0.8, lo que plantea la pregunta: ¿Cuál es el mejor valor para el factor de suavizado?
Estimando el mejor valor $\alpha$ de los datos.
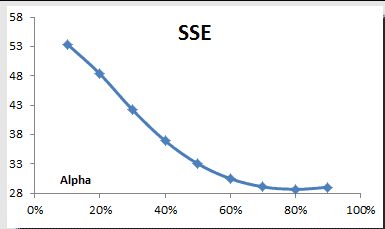
En la práctica, el parámetro de suavizado es escogido a menudo por una búsqueda de cuadrícula del espacio de parámetros; eso significa, que se prueban soluciones diferentes para $\alpha$ comenzando con esto, por ejemplo, $\alpha=0.1$ to $\alpha = 0.9$, con incrementos de 0.1. Entonces $\alpha$ es escogido para que produzca la suma más pequeña de cuadrado (or mean squares) for the residuals (Es decir, los valores observados menos pronósticos de un paso adelante); Esto significa que el error al cuadrado también se conoce como error cuadrático medio ex-post (ex-post ECM para abreviar).
Utilizando la función TSSUB (para calcular el error), SUMSQ, y las tablas de datos en Excel, nosotros calculamos la suma de los errores cuadráticos (SCE) y graficamos los resultados:
EL SCE alcanza su valor mínimo alrededor 0.8, Así que escogimos este valor para nuestro suavizado.
Tutorial Video
Ejemplos de Archivos
Haga clic en el botón a continuación para descargar el ejemplo de Suavizado exponencial simple de Brown.