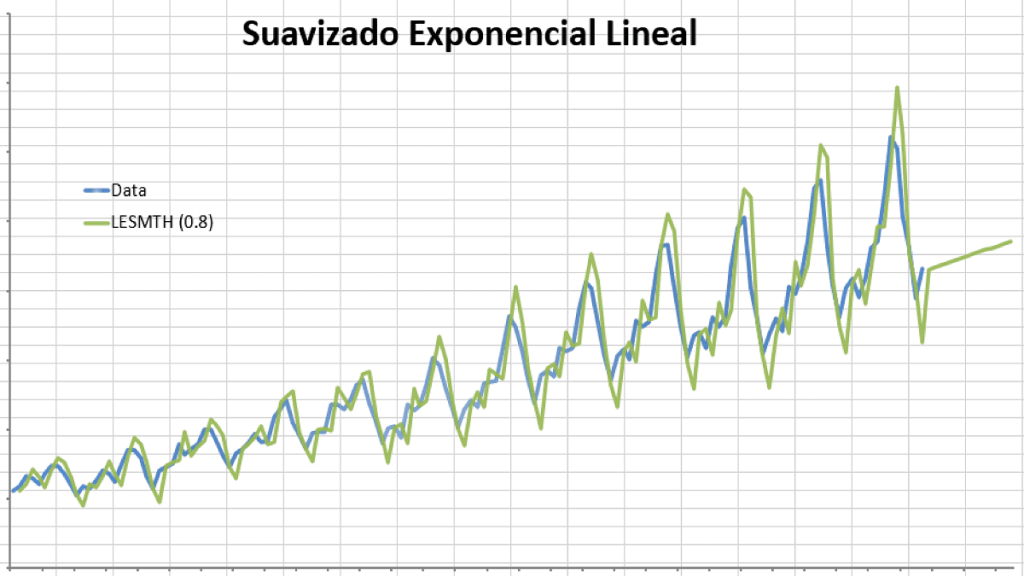
Suavizado Exponencial Lineal de Brown
Este es otro método de doble función de suavizado exponencial, pero tiene un factor de suavizado:
$S_1^{‘}=X_1$
$S_1^{”}=X_1$
$S_{t>1}^{‘}=\alpha X_t + (1-\alpha)S_{t-1}^{‘}$
$S_{t>1}^{”}=\alpha S_{t}^{‘}+(1-\alpha)S_{t-1}^{”}$
$a_{1<t<T}=2
S_{t}^{‘}-S_t^{”}$
$b_{1<t<T}=\frac{\alpha}{1-\alpha}\times (S_t^{‘}-S_t^{”})$
$Y_{T+m}=a_T+m\times b_T$
Donde:
- $\alpha$ is the smoothing factor ($0 \prec \alpha \prec 1$)
El doble suavizado exponencial de Brown toma un parámetro menor que la función de Holt-Winter, pero puede no ofrecer un ajuste tan bueno como esa función.
Ejemplo 1:
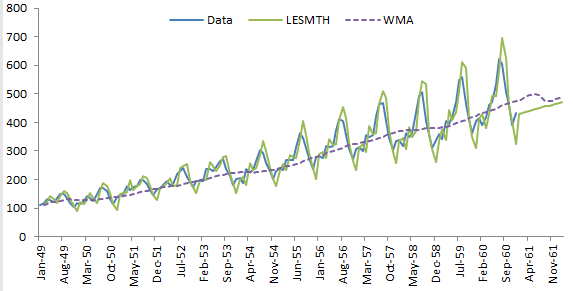
Utilicemos el mismo ejemplo en el exponencial doble de Holt-Winter y comparemos la suma óptima del error cuadrático.
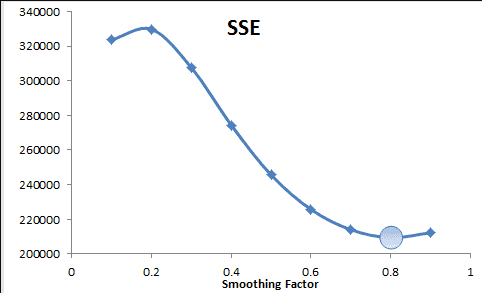
¿Cómo encontramos el mejor factor de suavizado ($\alpha$)?
Nosotros utilizamos el mismo método para seleccionar el valor alfa que minimiza la suma del error al cuadrado. Para los ejemplos de datos de ejemplo, se encuentra que el alpha es 0.8
Tutorial Video
Ejemplos de Archivos
Haga clic en el botón a continuación para descargar el ejemplo de suavizado exponencial lineal de Brown.