Suavizado Exponencial Doble de Holt
El suavizado exponencial simple no funciona bien en presencia de una tendencia, por lo que se proponen varios métodos concebidos bajo el paraguas “doble exponencial” para manejar este tipo de datos.
NumXL admite el doble suavizado exponencial de Holt-Winter, que toma la siguiente formulación:
$$S_1=X_1$$ $$B_1=\frac{X_T-X_1}{T-1}$$ $$S_{t>1}=\alpha X_t + (1-\alpha)(S_{t-1}+B_{t-1})$$ $$B_{t>1}=\beta (S_t – S_{t-1})+(1-\beta)B_{t-1}$$ $$Y_t=\left\{\begin{matrix} S_t+B_t & t<T\\ S_T+m\times B_T & t=T+m \end{matrix}\right.$$
Dónde
- $\alpha$ es el factor de suavizado ($0 \prec \alpha \prec 1$)
- $\beta$ es el factor de suavizado de tendencia ($0 \prec \beta \prec 1$)
Ejemplo 1:
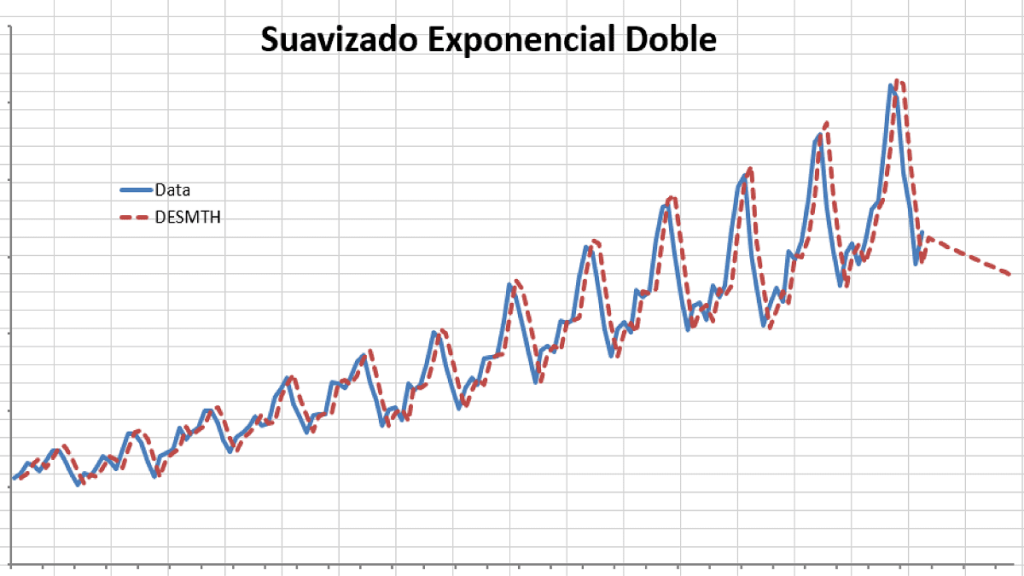
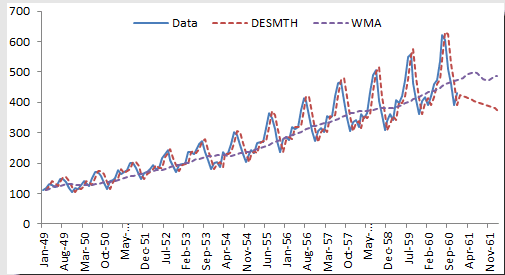
Examinemos los datos de las compañías aéreas internacionales de pasajeros
Se eligió un valor Alpha de 0,9 y un Beta de 0,1. Tenga en cuenta que aunque el suavizado doble traza bien los datos originales, el pronóstico fuera de la muestra es inferior al promedio móvil simple.
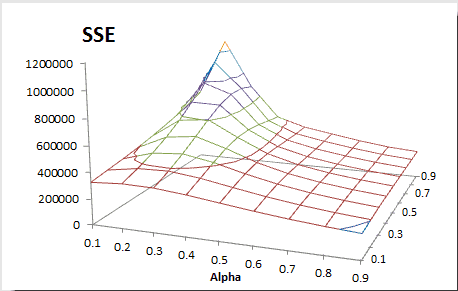
¿Cómo encontramos los mejores factores de suavizado?
Tomamos un enfoque similar a nuestro ejemplo simple de suavizado exponencial, pero modificado para dos variables. Nosotros calculamos la suma de los errores cuadráticos;construimos una tabla de datos de dos variables y seleccionamos los valores alfa y beta que minimizan el SCE general.