Prueba Dickey-Fuller Aumentada (ADF)
Durante los últimos meses, recibimos muchas consultas sobre la prueba estacionaria (aumentada) de Dickey-Fuller. Entonces, decidimos crear este artículo como una presentación completa sobre este tema.
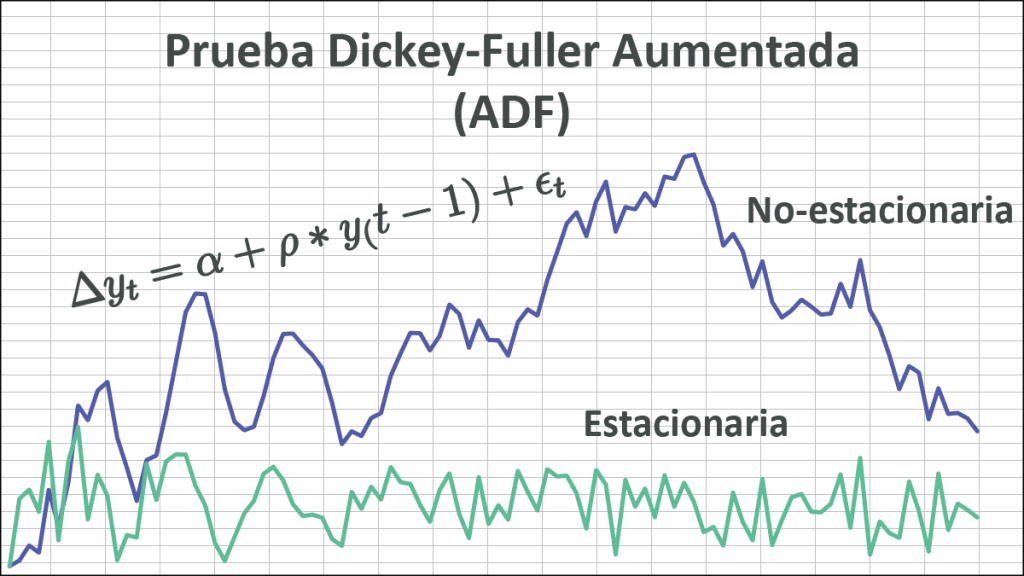
¿Qué es una serie temporal estacionaria? En términos simples, una serie de tiempo se llama estacionaria si no se desvía hacia el infinito y se mantiene alrededor de la media. Sus propiedades estadísticas (por ejemplo, momentos) no cambian con el tiempo.
¿Qué pasa con la tendencia? ¿Se considera que una serie temporal con tendencia no es estacionaria? No necesariamente. Las series de tiempo con tendencia determinista (es decir, no estocástica) se denominan series de tiempo estacionarias de tendencia; pero sólo si la serie de tiempo se mantiene alrededor de la línea de tendencia y no se desvía hacia el infinito.
¡Qué interesante! Entonces, ¿cómo probamos si tenemos una serie de tiempo estacionaria (o de tendencia estacionaria) o no? Alternativamente, podemos hacer una pregunta diferente: ¿qué causa la deriva no estacionaria? Una deriva estocástica (es decir, no estacionaria) proviene de la presencia de una raíz unitaria.
Para establecer el supuesto de estacionariedad, necesitamos rechazar la posibilidad de la presencia de raíz unitaria en la serie de tiempo.
¿De dónde viene la raíz unitaria? Una serie de tiempo no estacionaria se puede modelar como un modelo autorregresivo (AR) de orden uno (1) y un valor de coeficiente de uno (1).
$$y_t=\alpha+y_{t-1}+\epsilon_t$$
Prueba Dickey-Fuller (DF)
En la prueba de Dickey-Fuller, definimos el proceso subyacente de la siguiente manera:
Y se establece la siguiente prueba de hipótesis:
$$H_1=\rho<0$$
Al rechazar la hipótesis nula, estamos afirmando que la serie de tiempo no tiene raíz unitaria y, por lo tanto, es estacionaria.
Usando regresión lineal simple, podemos calcular el puntaje de la prueba para $\rho$, pero ¿cuál es la distribución subyacente de $\rho$? No es la distribución t de Student, por lo que debemos calcularla utilizando métodos de simulación.
Simulación: para un tamaño de muestra dado N (por ejemplo, 25),
- Simule una caminata aleatoria con una varianza de 1: $$y_t=y_{t-1}+ \epsilon\sim N\left(0,1\right)$$
- Ejecute la regresión lineal simple: $$\Delta y_t=\alpha+\rho\times y_{t-1}+\epsilon_t$$
- Calcule la puntuación de la prueba de $/rho$.
- Repita los pasos de 1 a 3.
Usando los valores simulados del puntaje de la prueba, construya la distribución y calcule los diferentes valores críticos (por ejemplo, 1%, 2.5%, 5%, 10%, etc.)
Usando las funciones de regresión lineal simple (SLR) de NumXL y el asistente de simulaciones de Monte-Carlo (MC), podemos generar la distribución subyacente por nosotros mismos.
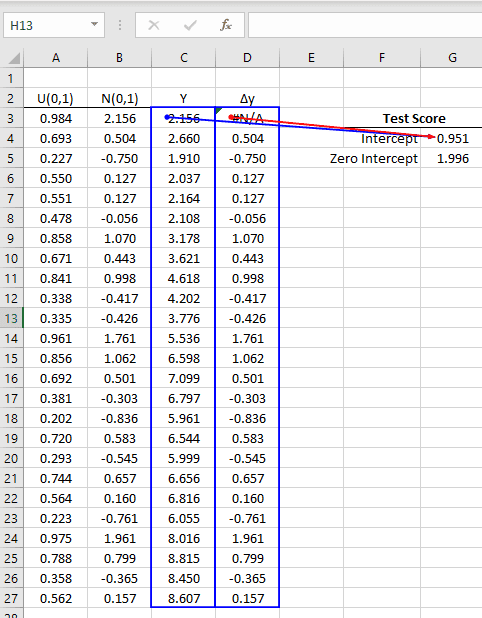
- Genere una caminata aleatoria (Y) de tamaño 25, con choques de varianza gaussiana de uno (1).
- Calcule la diferencia de primer orden de Y.
- Usando las funciones SLR, calcule el puntaje de la prueba para el coeficiente del 1er parámetro:
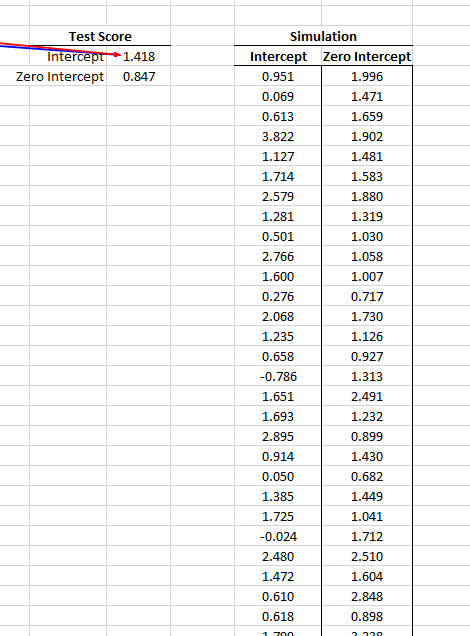
- Utilizando la simulación MC 1000 veces, almacene la puntuación de la prueba para ambos tipos de regresión (intersección cero y distinta de cero) en columnas vacías.
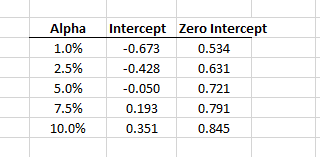
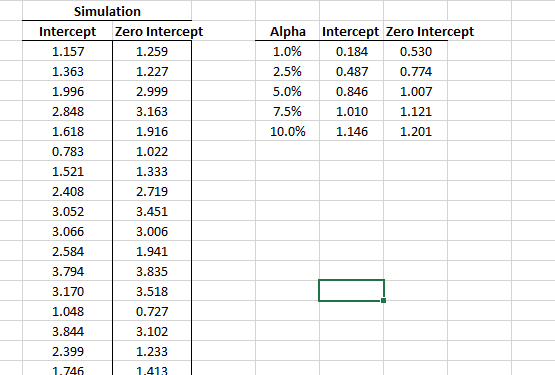
- Utilizando la función Cuantil(.), calcule los valores críticos (C.V.) para diferentes niveles de significación.
- Ahora, para un conjunto de datos dado de tamaño 25, ejecute una regresión similar y calcule el puntaje de prueba del valor del coeficiente.
- Compare la puntuación de la prueba de regresión con los valores críticos de la simulación.
- Para establecer la estacionariedad; el puntaje de la prueba debe ser menor que los valores críticos (arriba); para que podamos rechazar la hipótesis nula.
¿Qué pasa con el escenario de tendencia estacionaria? Necesitaríamos agregar un término de tendencia determinista en la regresión:
$$\Delta y_t=\alpha+\gamma\times t+\rho\times y_{t-1}+\epsilon_t$$
Para continuar con la simulación agregamos una columna constante para la tendencia temporal y calculamos el puntaje de la prueba para Y usando el modelo de regresión lineal múltiple (MLR).
Nuevamente, usando la simulación NumXL Monte-Carlo, generemos 1000 valores para los puntajes de la prueba y calculemos los valores críticos de puntaje de la prueba.
Prueba Aumentada de Dickey-Fuller (ADF)
La principal diferencia en la prueba de Dickey-Fuller aumentada es la complejidad añadida en el modelo de regresión.
$$\Delta y_t=\alpha+\rho\times y_{t-1}+\delta_1\Delta y_{t-1}+\cdots+\delta_p\Delta y_{t-p}+\epsilon_t$$
Al incluir retrasos de orden p en la formulación ADF, estamos permitiendo procesos AR de orden superior. Esto significa que el orden de retardo p debe determinarse al aplicar la prueba.
¿Cómo determinamos el valor de p? Un enfoque posible es comenzar con un valor más alto (p. ej., 5) y probar hacia abajo examinando la significancia estadística del coeficiente (es decir, el valor t).
Una vez que determinamos el p óptimo y calculamos la puntuación de la prueba del coeficiente de Y (es decir, 𝜌), los comparamos con los valores críticos de la prueba.
Los valores críticos de la prueba ADF se pueden calcular utilizando simulaciones de Monte-Carlo. Comenzamos con una muestra de caminata aleatoria de un tamaño determinado (por ejemplo, 25) y calculamos la puntuación de la prueba del coeficiente Y en el modelo de regresión lineal múltiple (MLR).
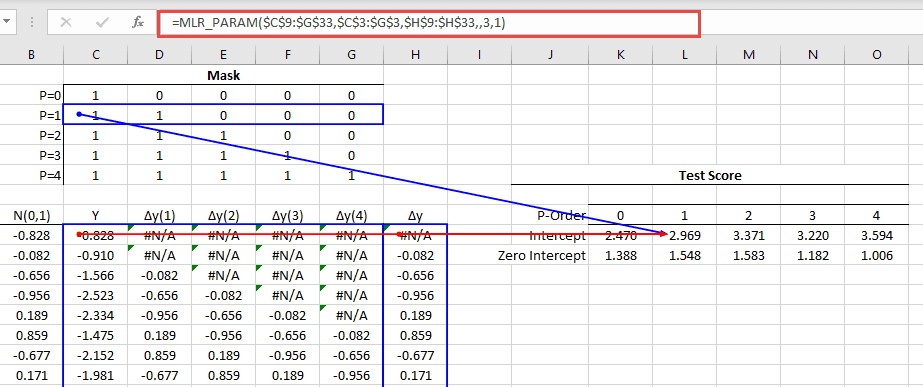
Usando la función NumXL MLR_PARAM(.), podemos calcular la puntuación de la prueba para diferentes valores de P alterando el argumento de la máscara.
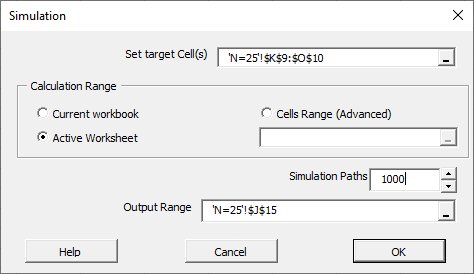
Ahora estamos listos para ejecutar la simulación Monte-Carlo en todos los modelos MLR.
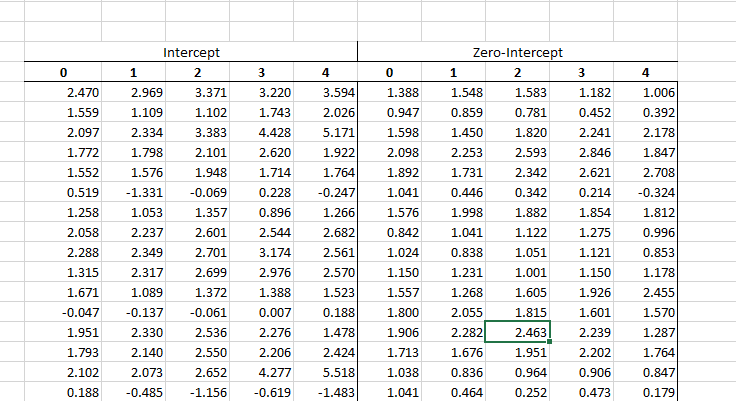
En el asistente de MC, especificamos toda la tabla como celdas de destino. El asistente de MC genera su salida escaneando las celdas de destino de izquierda a derecha, luego de arriba a abajo, y escribiendo sus valores en columnas adyacentes.
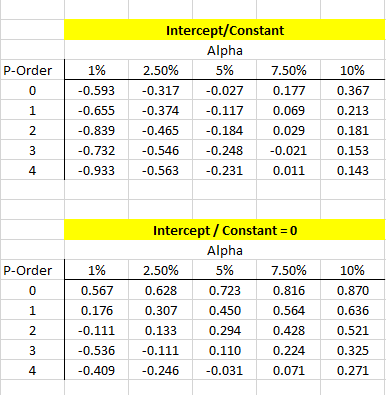
Usando los resultados de la simulación, podemos calcular el valor crítico de la prueba para N=25, diferentes valores de orden P y el nivel de significancia (entre 1 % y 10 %).
Tal como lo hicimos en la prueba original de Dickey-Fuller; para rechazar la hipótesis nula (presencia de raíz unitaria) necesitamos que la puntuación de la prueba de regresión del coeficiente Y sea menor que el valor crítico.
¿Qué pasa con la tendencia-estacionariedad? Para examinar la estacionariedad de la tendencia debemos incluir una variable de tendencia en el conjunto de datos; calcular la puntuación de la prueba para el coeficiente de Y e incluirla en la simulación.
Conclusión
En este artículo, describimos los supuestos subyacentes en las pruebas estacionarias y la mecánica para generar los valores críticos de la prueba para diferentes tamaños de muestra, niveles de significancia y modelos de regresión (por ejemplo, intercepción, tendencia) utilizando las funciones de Excel y NumXL.
Para demostrar la técnica de simulación, ejecutamos sólo 1000 simulaciones para generar los valores críticos. En la práctica, las simulaciones del orden de 2 millones arrojan valores críticos relativamente estables y son confiables para las inferencias de pruebas estadísticas.
Para obtener más información sobre la prueba ADF, visite nuestras páginas de la Guía del usuario o Manual de referencia del sobre el tema. Puede descargar una prueba gratuita de 14 días completamente funcional de NumXL para que usted mismo pruebe cualquiera de nuestras funciones.
Consulte las secciones Notas técnicas o Pruebas estadísticas para obtener más artículos que puedan interesarle.
Ejemplos de Archivos
Haga clic en el botón a continuación para descargar el ejemplo de prueba de Dickey-Fuller aumentada (ADF).