En esta entrada, examinaremos un caso inspirado por una discusión online con uno de los usuarios en nuestros foros de soporte: [Community Help]. El caso tiene que ver con la predictibilidad de la tasa de cierre diario EUR/USD , dada su historia previa.
Para empezar, hemos construido una estrategia donde compramos EUR a precio de mercado abierto y cerramos la posición (venta de EUR) a precio de mercado cerrado.
En el mercado de contado el FX EUR/USD es muy eficiente ya que los vendedores constantemente monitorean y explotan (ej. Arbitraje) cualquier información en las tasas de series de tiempo hasta que no es económico explotarlo más. Como resultado, pasa -sin que nos sorprenda mucho, que los datos de retorno diarios se ven muy parecidos a la distribución de ruido blanco. Esto da pie a la pregunta: ¿Qué sigue?
Asumiendo que nuestro objetivo principal para pronosticar una tasa de cierre del día siguiente de EUR/USD es generar ganancias, tomamos un abordaje levemente distinto y trazamos una estrategia con ajustes de interrupción de pérdida que no solamente limitan la pérdida diaria sino que también generan un retorno positivo.
This approach has proven to be more fruitful and will pave the way for many more improvements.
Análisis de Retornos Diarios
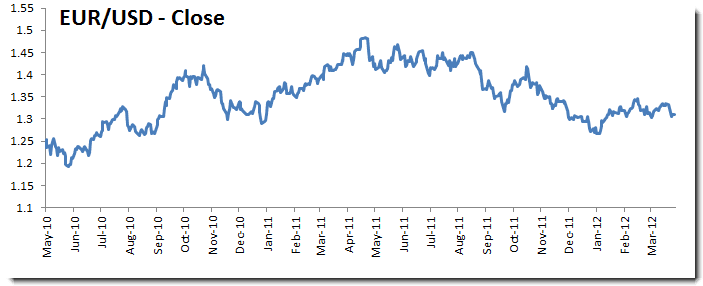
Para nuestros datos de muestra, usamos la tasa de cambio de FX de EUR/USD entre Marzo de 2010 a Abril 9 de 2012.
En esta entrada consideraremos una estrategia de comercialización que compra EUR (EUR = FX tasa en USD) en un mercado abierto (MOO) y cierra la posición (ej. ventas EUR) en el mercado cerrado (MOC).
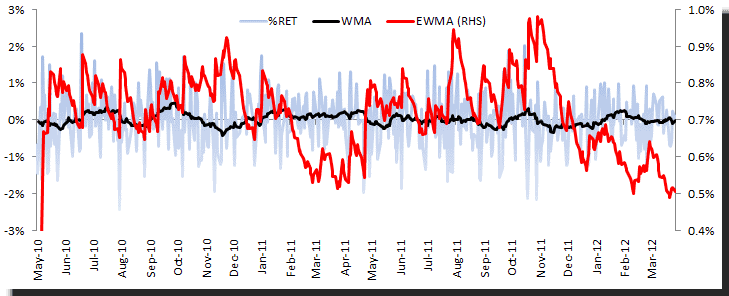
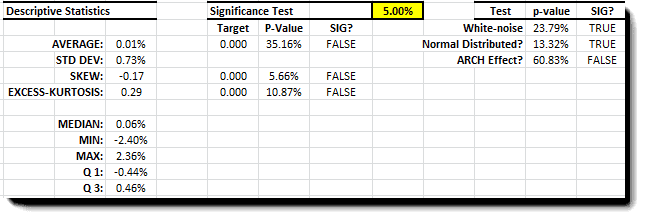
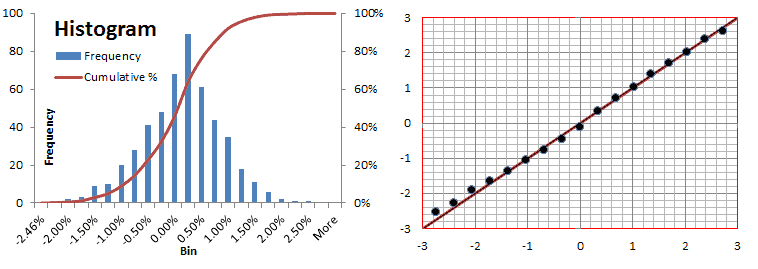
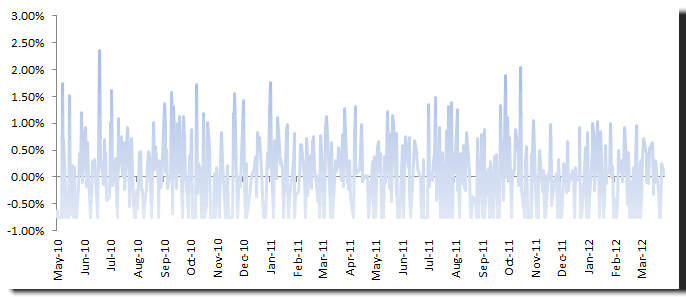
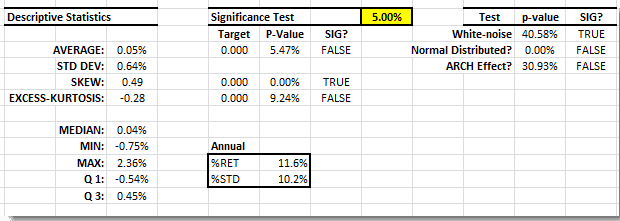
Las serie de retornos diarios muestra una media constante (proxy 20 por day WMA) y una volatilidad relativamente estable (0.5-1.0%). Examinando las estadísticas de resumen, el retorno promedio no es significativamente diferente de cero, con una distribución simétrica y colas de apariencia normal.
En la tabla final a la derecha podemos ver que los retornos diarios son más como la distribución Gaussiana y, por eso, no tienen información.
Discusión
Los retornos diarios actúan más como el ruido Gaussiano así que retornos pasados no revelan ninguna información que pueda ayudarnos a predecir mejor los puntos del futuro. ¿Qué tal técnicas de modelado no lineales (ej. Redes neurales, algoritmos genéticos)?
En mi opinión preferiría explorar y traer una nueva information al análisis que gastar mi tiempo usando técnicas sofisticadas de modelado. En nuestro análisis, tratamos de evadir la trampa del sobre-ajuste y de construir un modelo robusto para un pronóstico confiable.
Series de Tiempo Diarias de Máximos y Mínimos
Mientras restringimos nuestro análisis al mercado abierto y cerrado, que ocurre en momentos precisos del día, el HI y LO representan las tasas Máximas y Mínimas de las tasas internas diarias. Además, son imposibles de identificar con certeza , así que no podemos comerciar con ellas.
Sin embargo, las tasas diarias HI y LO proporcionan nueva información que no está todavía en las series de tiempo abiertas o cerradas; como resultado, podemos pronosticar sus niveles relativos en cierta medida.
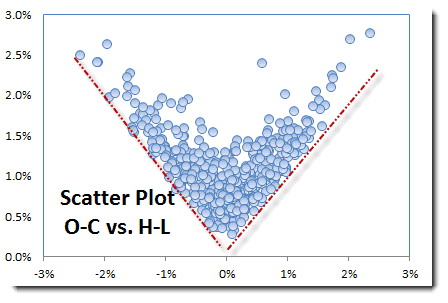
En la gráfica anterior, por favor note que los retornos HI-LO están relacionados con la volatilidad de los retornos abiertos y cerrados.
Usando los datos de la muestra, hemos implementado una orden de venta de fin de la pérdida con un nivel programado diariamente en un mercado abierto.
Definición: un freno en la pérdida para comprar o vender un bien (ej. Seguridad de comercio o mercancía) una vez el precio del activo alcanza un precio específico, conocido como precio con freno de la pérdida. Aquí se usa una orden de freno de venta para limitar la pérdida en un producto mercadeable que poseemos.
Usando la tasa diaria LO examinamos si el precio de freno se ha infringido por el día, si se ha infringido, programamos el precio de oferta como precio de freno (sin asumir descenso o tasas de transacción), de otra manera continuamos usando el precio cerrado del mercado por el precio de venta.
En este ejercicio examinamos las siguientes técnicas para frenar el precio: (1) porcentaje fijo por debajo del precio de apertura del mercado (ej. 0.75%), (2) compensación fija por debajo del precio de apertura del mercado.
1. El precio de freno se programa como un porcentaje fijo por debajo de la apertura del mercado
Examinando el resumen de estadísticas, los datos exhiben una desviación positiva y un promedio marginalmente significativo.
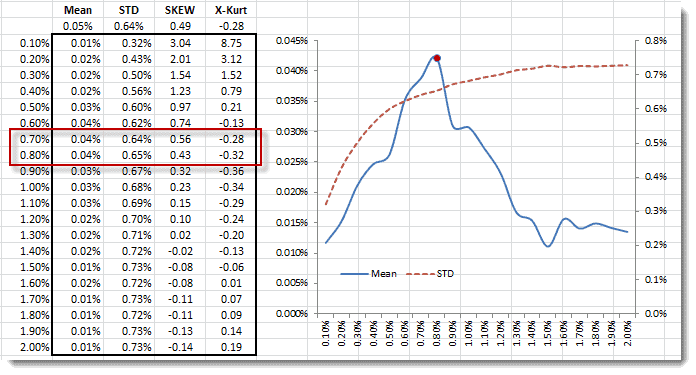
Para optimizar la configuración del porcentaje del precio de freno, hemos construido una tabla de datos donde variamos el porcentaje entre 0.1% y 2%.
Graficando la media y la volatilidad de la estrategia de comercio, escogimos 0.75% como la mejor opción. Esta configuración da a la nueva estrategia de comercio un retorno annual de 11.6% y una volatilidad de 10.2%. Además, los retornos de la nueva estrategia actúan como el sonido blanco (pero no Gaussiano), así que no hemos dejado ninguna información en la tabla.
2. El precio de freno está configurado como una compensación por debajo de la apertura del mercado.
En un intento por mejorar la estrategia de precio de freno, usamos el estimado EWMA y el WMA de HI-LO. Seguimos los mismos pasos: generar estrategias de retorno, usar una tabla de datos para examinar diferentes configuraciones y, finalmente, escoger la mejor. Los resultados se comparan con uno muy simple que hemos ilustrado arriba.
Para análisis detallado e ilustración, por favor referirse al archivo de la tabla de Excel (disponible online).
Conclusión
Hasta el momento, empezamos de una muestra de datos de ruido Gaussiano, hemos incorporado diariamente tasas LO, y concebido una nueva estrategia con freno de perdida que no sólo limita la pérdida diaria sino que genera retornos positivos.
Adicionalmente, podemos concebir otra estrategia que emplea una orden de límite de venta para bloquear ganancias. Usando el diario HI podemos examinar si se ha infringido el precio límite y construir nuevas estrategias de retorno.
¿Qué tal una estrategia que emplee ambas: freno de pérdida y límite de orden? Desafortunadamente, el conjunto de datos que tenemos no contiene información acerca de si HI ocurre antes o después de LO ese día.
La moraleja aquí es que podemos empezar con una serie de datos que ya no se parezca al ruido blanco Gaussiano, pero que con la introducción de nueva información (ej. HI y LO diarios, volumen, paridad de tasa de interés, eventos cumbre de G8, etc) podamos derivar una nueva serie de tiempo con características más favorables.