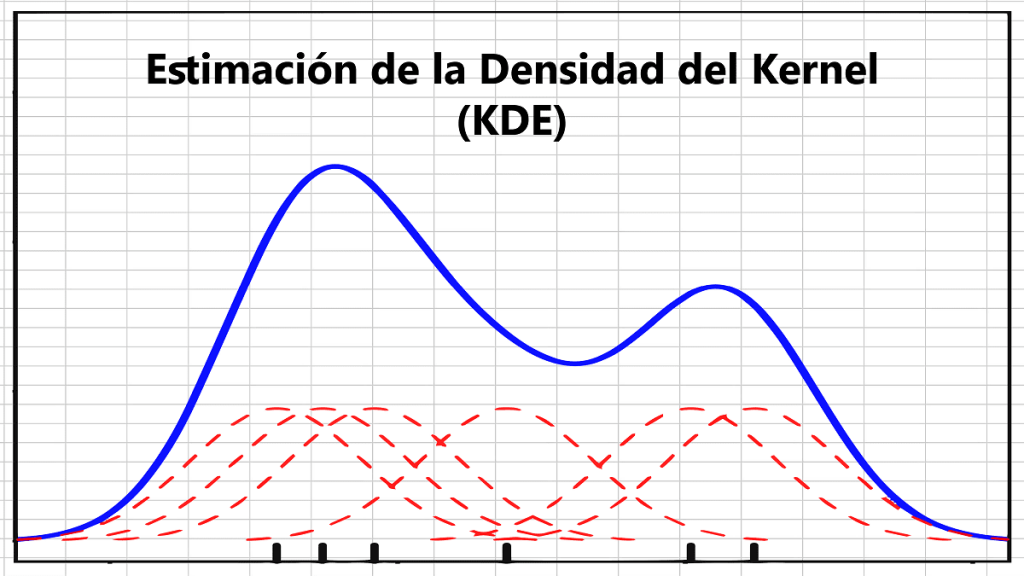
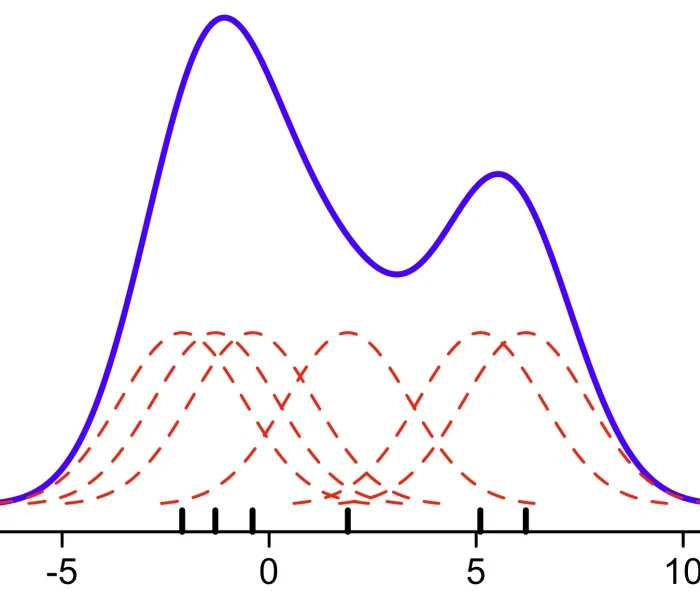
Estimación de la Densidad del Kernel (KDE)
Anteriormente, hemos visto cómo utilizar el método del histograma para inferir la función de densidad de probabilidad (PDF) de una variable aleatoria (población) con una muestra finita de datos. En este tutorial, te llevamos en el problema de la inferencia de la función de densidad de probabilidad, pero utilizando otro método: estimación de densidad de Kernel.
La estimación de densidad de Kernel. están estrechamente relacionados con histogramas, pero puede ser dotado de propiedades tales como suavizado o continuidad mediante el uso de un núcleo adecuado.
¿Por qué nos importa?
Resumen
Consideremos una muestra de datos finitos $\{x_1,x_2, \cdots ,x_N\}$ observado de un proceso estocástico (es decir, continuo y aleatorio). Deseamos inferir la función de densidad de probabilidad de la población.
En el método del histograma, seleccionamos el límite izquierdo del histograma $(x_o)$, el ancho de la celda (h), y luego calculamos la celda k estimadora de probabilidad $f_h(k)$:
- El bin o celda k representa el siguiente intervalo$[x_o+(k-1)h, x_o+k\times h)$
- $\hat f_h(k)=\frac{\sum_{i=1}^N I\{(k-1)h\leq x_i-x_o\leq k\times h)\}}{N}$
- $I\{.\}$ es una función del evento que devuelve 1 (uno) si la condición es verdadera,de lo contrario 0 (cero).
La elección de las celdas, especialmente el anchura de la celda (h), tiene un efecto substancial en la forma y otras propoiedades de $f_h(k)$.
Finalmente, podemos pensar en el método del histograma de la siguiente manera:
- Cada observación (evento) es estadísticamente independiente de todos los otros, y su probabilidad de ocurrencia es igual a $\frac{1}{N}$.
- $f_h(k)$ es simplemente la suma integral de las probabilidades del evento en cada celda
Qué es un kernel?
Un kernel es una función no negativa, con valores reales, integrable K(.) satisfaciendo los dos siguientes requerimientos:
$$\int_{-\infty}^{\infty}K(u)du=1$$
$$K(u)=k(-u)$$
Y, como resultado, la función de escalada $K^*(u)$, donde $K^*(u)=\lambda K(\lambda \times u)$, es un núcleo también.
Ahora, ubica una función escalada kernel a cada observación en la muestra y calcula los nuevos estimadores de probabilidad $f_h(x)$ para un valor x (en comparación con un bin anterior en el histograma).
$$\hat f_h(x)=\frac{1}{N}\sum_{i=1}^N K_h(x-x_i)$$
$$K_h(u)=\frac{1}{h}K(u/h)$$
$$\hat f_h(x)=\frac{1}{N\times h}\sum_{i=1}^N K((x-x_i)/h)$$
Nota: Para el núcleo Gausianno, el ancho de banda es el mismo que la desviación estándar de $(x-x_i)$.
$$P(x)=\left\{\begin{matrix} \frac{1}{N} & x \in \{x_1,x_2,\cdots , x_N\} \\ 0 & x \notin \{x_1,x_2,\cdots , x_N\} \end{matrix}\right.$$
Con la función núcleo.Esto permite superposición entre los núcleos, promoviendo así la continuidad en el estimador de probabilidad.
Por qué KDE?
Debido a muestra muestra de datos,nos quedamos con un conjunto finito de valores para variables aleatorias continuas. El uso de un núcleo en vez de probabilidades discretas, promovemos la natural continuidad en la variable aleatoria subyacente.
Cuál núcleo debo yo utilizar?
Un rango de funciones núcleo son comúnmente utilizadas: uniforme, triangular,
biweight, triweight y Epanechnikov. El núcleo es usualmente utilizado; $K(.)=\phi(.)$,
donde $\phi$ es la función de densidad normal estándar.
Cómo yo puedo calcular apropiadamente el ancho de banda del núcleo?
Intuitivamente, uno quiere elegir un h tan pequeño como los datos permite, pero hay una compensación entre el sesgo del estimador y su varianza.
La selección del ancho de banda de un estimador de núcleo es un tema de investigación considerable. Vamos a describir dos métodos populares:
- La selección subjetiva – Uno puede experimentar mediante el uso de diferentes anchos de banda y simplemente seleccionando uno que “se ve bien” para el tipo de datos bajo investigación
- Selecciona con referencia a algunos distribución dada – Aquí se selecciona
el ancho de banda que sería óptimo para un PDF particular. Tenga en cuenta
que no se está asumiendo que $f(x)$ es normal, pero en lugar de seleccionar
una h la cual podria ser optima si el PDF fuera normal. Usando un
núcleo Gaussiano, el ancho de banda óptimo $h_{opt}$ es definido de la siguiente
manera:
$$h_{opt}=\sigma\times \sqrt[5]{\frac{4}{3N}}$$
La distribución normal no es una distribución “ondulada”; es unimodal y con forma de campana.Por lo tanto es de esperar que $h_{opt}$ será demasiado grande para distribuciones multimodales. Además, la varianza de la muestra ($s^2$) no es un estimador robusto de $\sigma^2$; sobreestima si algunos valores atípicos extremos (observaciones) están presentes. Para superar estos problemas, Silverman propone el siguiente estimador de ancho de banda:
$$h_{opt}=\frac{0.9\times \hat\sigma}{\sqrt[5]N}$$
$$\hat \sigma = \textrm{min}(s,\frac{R}{1.34})$$
$$R=IQR=Q3-Q1$$
Donde IQR es el rango intercuartil y “s” es la desviación estándar de la muestra. - Basada en los datos de estimación – esta es un área de investigación actual utilizando varios métodos diferentes: transformada de Fourier, basada en difusión, etc..
Conclusión
En este tutorial, hemos demostrado el proceso para generar una estimación de la densidad del núcleo en Excel usando las funciones de complemento de NumXL.
¿A dónde vamos desde aquí?
En primer lugar, para responder a la cuestión de optimalidad, necesitamos introducir algoritmos adicionales para estimar sus valores. Por ejemplo, en “Anales de Estadística, Volumen 38, Número 5, páginas 2916-2957”, Z. I. Botev, J. F. Grotowski, y D. P. Kroese describieron un método basado en datos de ejemplos numéricos para encontrar el ancho de banda óptimo utilizando una estimación de la densidad del núcleo.
Ejemplos de Archivos
Haga clic en el botón a continuación para descargar el ejemplo de Estimación de la densidad del kernel (KDE).