Modelo ARMA Desconectado
Esta es la primera entrada de nuestra serie de modelado ARMA, en la que profundizamos en los detalles de cada uno de los modelos de series de tiempo con los que ya están familiarizados, destacando las suposiciones subyacentes y aterrizando las intuiciones detrás de ellas.
En esta edición, abordamos el modelo ARMA – una piedra angular en el modelado de las series de tiempo. A diferencia de los problemas de análisis anteriores, comenzaremos aquí con la definición del proceso ARMA, declararemos las entradas, salidas, parámetros, restricciones de estabilidad, supuestos y, finalmente, dibujaremos algunas pautas para el proceso de modelado.
Antecedentes
Por definición, el promedio móvil autorregresivo, (ARMA) es un proceso estocástico estacionario, compuesto por sumas de Excel autorregresivas y componentes de media móvil.
Alternativamente, en una formulación simple:
$$y_t-\phi _1y_{t-1}-\phi _2y_{t-2}-…-\phi_py_{t-p}=\mu +a_t+\theta _1 a_{t-1}+\theta _2 a_{t-2}+…+\theta _q a_{t-q}$$ $$OR$$ $$y_t=\mu +(\phi _1y_{t-1}-\phi _2y_{t-2}-\phi_py_{t-p})+(\theta _1 a_{t-1}+\theta _2 a_{t-2}+\theta _q a_{t-q})+a_t$$
Donde:
- $y_t$ es la salida observada en el tiempo t.
- $a_t$ es el término de innovation, choque o error en el tiempo t.
- $\left \{ a_t \right \}$ Observaciones de series de tiempo:
- Son independientes e idénticamente distribuidos $(a_t\sim i.i.d)$
- Sigue una distribución Gaussiana $(i.e. \Phi (0,\sigma ^2))$
La varianza de las distribuciones de choques (es decir. $\sigma^2$) es invariante en el tiempo.
Usando anotaciones en negro (i.e. $L$), podemos expresar el proceso ARMA de la siguiente manera.
$$(1-\phi _1L-\phi_2L^2-…-\phi_pL^p)(y_t-\mu )=(1-\theta_1L-\theta _2L^2-…-\theta_pL^p)a_t$$
Suposiciones
Veamos más de cerca la fórmula. El proceso ARMA es simplemente una suma ponderada de las observaciones de la producción pasada y los choques, con pocas suposiciones clave:
- El proceso ARMA genera una serie de tiempo estacionaria ($\left \{ y_t \right \}$).
- Los residuales $\left \{ a_t \right \}$ siguen una distribución Gaussiana estable.
- Los parámetros de los componentes $\left \{ \phi _1,\phi_2,…,\phi_p,\theta _1,\theta_2,…,\theta_p \right \}$ los valores son constantes.
- Los valores de parámetro $\left \{ \phi _1,\phi_2,…,\phi_p,\theta _1,\theta_2,…,\theta_p \right \}$ generan un proceso estacionario ARMA.
Un proceso estocástico es una contrapartida de un proceso determinista; describe la evolución de una variable aleatoria en el tiempo. En nuestro caso, la variable aleatoria es $y_t$
Entonces, ¿Son los valores $\left \{ y_t\right \}$ independientes? ¿Están estos idénticamente distribuidos? Y si lo están, $y_t$ no deben ser descritos por un proceso estocástico, sino por un modelo de distribución probabilística.
Para casos donde $\left \{ y_t\right \}$ los valores no son independientes (Por ejemplo el valor $y_t$ es dependiente de la ruta.), un modelo estocástico SIMILAR a ARMA se usa para captar la evolución de $y_t$.
El proceso ARMA sólo captura la correlación serial (es decir, autocorrelación) entre las observaciones. En términos simples, el proceso ARMA resume los valores de observaciones pasadas, no sus valores cuadrados o sus logaritmos, etc. La dependencia de orden superior requiere un proceso diferente (por ejemplo, ARCH/GARCH, modelos no lineales, etc.).
Existen numerosos ejemplos de un proceso estocástico en el que los valores pasados afectan a los actuales. Por ejemplo, en una oficina de ventas que recibe pedidos de cotizaciones (RFQs) en forma continua, algunas se realizan como ventas ganadas, algunas como ventas perdidas, y algunas ocurren en el próximo mes. Hay numerosos ejemplos de un proceso estocástico donde los valores pasados afectan los actuales. Como resultado, en cualquier mes algunas de los casos de ventas ganadas se originan como pedidos de cotizaciones o son ventas repetidas del mes anterior.
¿Qué son los choques, innovaciones o términos de error?
Esta es una pregunta difícil y la respuesta no deja de confundir. Sin embargo, vamos a intentarlo: En palabras sencillas, el término de error en un modelo dado es un balde que recoge todo para todas las variaciones que el modelo no explica.
¿Confundido? Digámoslo de otra manera. En cualquier sistema dado, posiblemente existen decenas de variables que afectan la evolución de $ y_t $, pero el modelo captura pocas de ellas y agrupará el resto como un término de error en su fórmula (es decir. $a_t$ ).
¿Todavía perdido? Vamos a usar un ejemplo. Para un proceso de precio de acciones, hay posiblemente cientos de factores que conducen el precio al alza o a la baja, incluyendo:
- Anuncios de repartición de dividendos
- Reportes trimestrales de ganancias
- Actividades de fusiones y adquisiciones (M&A)
- Eventos legales, por ejemplo, la amenaza de demandas colectivas.
- Otros
Un modelo, por diseño, es una simplificación de una realidad compleja. Cualquier cosa que dejemos por fuera del modelo se incluye automáticamente en el término de error.
El proceso ARMA supone que el efecto colectivo de todos esos factores actúa más o menos como el ruido gaussiano.
A diferencia de un modelo de regresión, la aparición de un estímulo (por ejemplo, choques) puede tener un efecto en el nivel actual, y posiblemente en los niveles futuros. Por ejemplo, un evento corporativo (por ejemplo, la actividad de funciones & amp; adquisiciones) afecta el precio de las acciones de la empresa subalterna, pero el cambio puede tomar algún tiempo para tener su impacto completo, ya que los participantes del mercado absorben/analizan la información disponible y reaccionan en consecuencia.
Esto plantea la pregunta: ¿los valores pasados de la producción ya no tienen la información pasada de los choques?
Sí, la historia de los choques ya está contabilizada en los niveles de producción pasados. Un modelo ARMA puede ser representado solamente como un modelo auto-regresivo puro (AR), pero el requisito de almacenamiento de tal sistema en infinito. Esta es la única razón para incluir el componente MA: ahorrar en almacenamiento y simplificar la formulación.
$$(1-\phi _1L-\phi_2L^2-…-\phi_pL^p)(y_t-\mu )=(1-\theta_1L-\theta _2L^2-…-\theta_pL^p)a_t$$ $$\frac{(1-\phi _1L-\phi_2L^2-…-\phi_pL^p)}{(1+\phi _1L+\phi_2L^2+…+\phi_pL^p)}(y_t-\mu )=a(t)$$ $$(1-\psi _1L-\psi _2L^2-\psi_3L^3-…-\psi_NL^N-…)(y_t-\mu )=a_t$$
Máquina ARMA
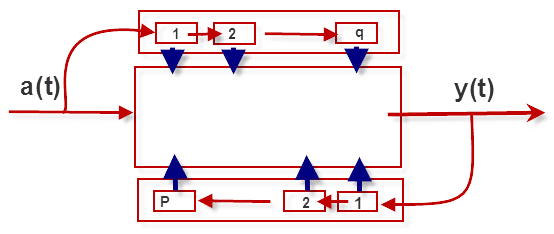
El proceso ARMA es una máquina simple que conserva información limitada sobre sus salidas pasadas y los choques que ha experimentado. Desde un punto de vista más sistemático, el proceso o máquina ARMA puede verse a continuación:
En esencia, la implementación física de un proceso ARMA (P,Q) requiere almacenamiento P+Q, o los requisitos de memoria de un ARMA (P, Q) son finitos (P+Q).
En el momento cero (0), la máquina ARMA y su almacenamiento son restablecidos. (es decir.$\left \{S_1^y,S_2^y,…,S_p^y,S_1^a,S_2^a,…,S_q^a \right \}$) son fijados en cero. Como nuevos choques (es decir. $a_t$) comienzan a llegar a nuestro sistema, los almacenamientos internos son actualizados con las nuevas salidas observadas ($y_t$) y choques realizados.
Además, el componente AR en el ARMA representa una retroalimentación positiva (sumando la suma ponderada de la salida pasada), y esto puede hacer que la salida sea no estacionaria. El efecto de retroalimentación para los choques es menos preocupante, ya que los choques tienen media cero y son independientes.
Para un proceso ARMA estable (es decir, estacionario), las raíces de la ecuación característica AR deben ser dentro de un círculo unitario.
$$1-\phi _1L-\phi_2L^2-…-\phi_pL^p=(1-\gamma _1L)(1-\gamma_2L)…(1-\gamma_p L)$$ $$\left | \gamma_k \right |< 1$$
Donde:
- $\gamma_k$ is the k-th root.
- $1\leq k\leq p$
En el evento en que los componentes MA y AR, tienen una raíz común, las órdenes ARMA deben ser reducidas.
ARMA Estacionario
Ahora tenemos un proceso ARMA estacionario estable, Cambiemos de marcha y examinemos las características de la serie de salida.
$$y_t-\phi _1y_{t-1}-\phi_1y_{t-2}-…-\phi_py_{t-p}=\mu +a_t+\theta _1a_{t-1}+\theta _2a_{t-2}+…+\theta _qa_{t-q}$$
Media marginal (media de largo plazo)
$$E\left [ y_t \right ]=E\left [ \mu +\phi _1y_{t-1}+\phi_1y_{t-2}+…-\phi_py_{t-p}+a_t+\theta _1a_{t-1}+\theta _2a_{t-2}+…+\theta _qa_{t-q} \right ]$$ $$E\left [ y_t \right ]= \mu +\phi _1E\left [y_{t-1} \right ] +\phi _2E\left [y_{t-2} \right ]+…+\phi _pE\left [y_{t-p} \right ]$$ $$E\left [ y_t \right ]= \frac{\mu }{1-\phi _1-\phi_2-…-\phi_p}$$
Para un proceso ARMA estacionario, la $\sum_{k-1}^{p}\phi_k\neq1$
Varianza marginal (varianza de largo plazo)
La fórmula para la varianza a largo plazo de un modelo ARMA es más complicada: para resolverlo, debemos derivar la representación MA del proceso ARMA, y luego tomar de ahí la varianza ya que todos los términos son independientes.
Por ejemplo, vamos a considerar el proceso ARMA (1, 1):
$$(1-\phi L)(y_t-\mu)=(1+\theta L)a_t$$ $$y_t-\mu=\frac{1+\theta L}{1-\phi L}a_t=(1+(\phi+\theta)L+\phi(\phi+\theta)L^2+\phi^2(\phi+\theta)L^3+…+\phi^{N-1}(\phi+\theta)L^N+…)a_t$$ $$y_t-\mu=a_t+(\phi+\theta)a_{t-1}+\phi(\phi+\theta)a_{t-2}+…+\phi^{N-1}(\phi+\theta)a_{t-n}+…$$ $$Var\left [ y_t-\mu \right ]=Var\left [ y_t \right ]=(1+(\phi+\theta)^2+\phi^2(\phi+\theta)^2+…+\phi^{2N-2}(\phi+\theta)^2+…) \sigma _a^2$$ $$Var\left [ y_t\right ]=Var\left [ y_t \right ]=(1+(\phi+\theta)^2(1+\phi^2+\phi^4+…+\phi^{2N-2}+…))\sigma _a^2=(1+\frac{(\phi+\theta)^2}{1-\phi^2})\sigma _a^2$$ $$\sigma_y^2=(\frac{1+2\theta\phi+\theta^2}{1-\phi^2})\sigma_a^2$$
Una vez más el proceso ARMA debe ser estacionario para que exista la varianza marginal (incondicional).
En mi discusión anterior, no estoy haciendo una distinción entre simplemente la ausencia de una raíz unitaria en la ecuación característica y la estacionalidad del proceso. Están relacionadas, pero la ausencia de una raíz unitaria no es una garantía de estacionalidad. Aún así, la raíz unitaria debe estar situada dentro del círculo unitario para ser precisa.
Conclusión
Repasemos lo que hemos hecho hasta ahora. Primero examinamos un proceso estacionario ARMA, junto con su formulación, entradas, suposiciones y requisitos de almacenamiento. A continuación, mostramos que un proceso ARMA incorpora sus valores de salida (autocorrelación) y los choques que experimentó anteriormente en la salida actual. Finalmente, se demostró que el proceso estacionario ARMA produce una serie de tiempo con una media y una varianza estables.
En nuestro análisis de datos, antes de proponer un modelo ARMA, debemos verificar el supuesto de estacionalidad y los requisitos de memoria finita.
- En el caso de que la serie de datos muestre una tendencia determinista, necesitamos eliminarla primero y luego usar los residuales para ARMA.
- En el caso de que el conjunto de datos exhiba una tendencia estocástica (por ejemplo, paseo aleatorio) o la estacionalidad, necesitamos considerar ARIM/SARIMA.
- Finalmente, el correlograma (es decir. ACF/PACF) pueden ser utilizados para medir el requerimiento de memoria del modelo; nosotros debemos esperar que ACF o PACF se desintegren rápidamente después de unos pocos retrasos. De lo contrario, esto puede ser un signo de no estacionalidad o un patrón a largo plazo (por ejemplo, ARFIMA).