Modelo ARIMA al Rescate
Esta es la segunda entrada de nuestra serie de modelado ARMA, en los que profundizamos en los detalles de cada uno de los modelos de series de tiempo con los que ya estarán ustedes familiarizados; destacando los supuestos subyacentes y conduciendo a casa las intuiciones detrás de ellos.
En series de tiempo financieras y otros campos, a menudo nos enfrentamos a series temporales no estacionarias, por ejemplo, niveles de precios negociados (por ejemplo, acciones, bonos, mercancías, etc.). En este caso, la serie de tiempo muestra ya sea tendencias, estacionalidad o simplemente un paseo aleatorio erróneo. Desafortunadamente, la mayor parte de las series de tiempo y los métodos econométricos sólo se pueden aplicar a los procesos estacionarios. ¿Cómo manejamos este escenario?
En este número abordamos el modelo ARIMA, una extensión del modelo ARMA, pero el modelo ARIMA se aplica a series de tiempo no estacionarias, el tipo de series temporales con una o más raíces unitarias (integradas).
Una vez más, comenzaremos aquí con la definición de proceso de ARIMA Excel, indicando las entradas, salidas, parámetros, restricciones de estabilidad y suposiciones. Luego introduciremos al operador de integración y dibujaremos algunas pautas para el proceso de modelado.
Antecedentes
Una serie de tiempo no estacionaria a menudo muestra unos pocos patrones comunes incluyendo tendencia a través del tiempo, estacionalidad y paseo aleatorio erróneo. La tendencia de estacionalidad puede ser también clasificada bien sea como determinista (función de tiempo) o estocástica (función de los valores pasados).
Para la tendencia estocástica y/o la estacionalidad, a menudo diferenciamos (es decir, calculamos el cambio de) la serie temporal original para inducir una serie estacionaria que puede ser modelada adicionalmente por un tipo de proceso ARMA.
Por definición, el proceso de movimiento promedio auto-regresivo integrado es un proceso ARMA para las series de tiempo diferenciadas.
Alternativamente, en una formulación simple, un ARIMA (p,d,q) se define de la siguiente manera:
$$\left(1-\sum_{i=1}^p{\phi_i L^i} \right )(1-L)^d Y_t =\mu + \left(1+ \sum_{j=1}^q{\theta_j L^j} \right )a_t$$
O
$$\left(1-\sum_{i=1}^p{\phi_i L^i} \right )Z_t = \mu + \left(1+ \sum_{j=1}^q{\theta_j L^j} \right )a_t$$ $$\left(1-\sum_{i=1}^p{\phi_i L^i} \right )(Z_t-\mu) = \left(1+ \sum_{j=1}^q{\theta_j L^j} \right )a_t$$ $$Z_t=\Delta^d Y_t=(1-L)\times(1-L)\times \cdots \times (1-L) Y_t=(1-L)^d Y_t$$
Donde:
- $Y_t$ Es la salida observada en el tiempo t.
- $\Delta^d$ Es el operador de la diferencia de orden d.
- $Z_t$ es la serie de tiempo diferenciada en el tiempo.
- $a_t$ es la innovation, choque o termino de error en el tiempo t.
- ${a_t}$ observaciones de las series de tiempo:
- Son independientes e idénticamente distribuidos
- Sigue una distribución Gaussiana (i.e. $\Phi(0,\sigma^2)$).
Suposiciones
Observando más de cerca la formulación, vemos que el proceso de ARIMA Excel es esencialmente un proceso ARMA para las series temporales diferenciadas aparte del operador de diferencia ($\Delta^d$). La misma suposición para un proceso de ARMA se aplica también aquí:
- El proceso ARMA genera una serie temporal estacionaria $Z_t$.
- Los residuales ${a_t}$ siguen una distribución Gaussiana estable.
- El parámetro del componente $\{\phi_1,\phi_2,\cdots,\phi_p,\theta_1,\theta_2,\cdots,\theta_q\}$ values are constants.
- El parámetro $\{\phi_1,\phi_2,\cdots,\phi_p,\theta_1,\theta_2,\cdots,\theta_q\}$ de los valores produce un proceso estacionario.
Suena simple? Sí lo es! Una selección cuidadosa de los parámetros del modelo ARMA puede garantizar un proceso estacionario para la diferencia de las series de tiempo diferenciada ($Z_t$), Pero ¿cómo interpretamos el pronóstico de $Y_t$ utilizando $Z_t$.
Operador de Integración (Sin Diferencia)
En muchos casos nosotros aplicamos un operador de diferencia para obtener una serie temporal estacionaria que puede ser fácilmente modelada usando el modelo ARMA. Pero, ¿cómo volver al espacio original de series temporales no diferenciadas e interpretar los resultados ARMA (por ejemplo, el pronóstico)? Nuestra mejor opción es utilizar el Operador de Integración.
DEFINICION: una serie de tiempo estocástica $\{Y_t\}$ se dice que es integrador de orden (d) (i.e. $Y_t\sim I(d)$) si las series temporales d-veces diferenciadas producen una representación ARMA invertible.
$$a_t=\frac{1-\sum_{i=1}^p {\phi_i L^i}}{1-\sum_{j=1}^q {\theta_j L^j}}\Delta^d Y_t =\frac{1-\sum_{i=1}^p {\phi_i L^i}}{1-\sum_{j=1}^q {\theta_j L^j}} Z_t=(1+\sum_{i=1}^\infty \pi_i L^i)Z_t$$ $$\sum_{i=1}^\infty {\left | \pi_i \right |}< \infty$$
e implícitamente;
$$\left(1-L\right)^d Y_t \sim \textrm{stationary}$$
Ahora, para recuperar $Y_t$ de las $(1-L)^d Y_t$, Aplicamos el operador de diferencia (integración).
Una integración de primer orden puede expresarse como:
$$Y_t=\frac{Z_t}{1-L}=Z_t \times (1+L+L^2+L^3+\cdots)=Z_t\sum_{i=0}^\infty L^i$$ $$Y_t=\sum_{i=0}^\infty Z_{t-i}$$ $$Y_{T+n}=Y_T + \sum_{i=1}^n Z_{T+i}$$
For higher order (i.e.$d$-order) integration, we simply integrate multiple times:
$$Y_t=\frac{Z_t}{(1-L)^d}=Z_t\times \frac{1}{1-L}\times \frac{1}{1-L}\times \cdots \times \frac{1}{1-L} = Z_t\times \left(\sum_{i=0}^\infty L^i \right )^d$$
Por ejemplo, para $d=2$, la integración del operador se define de la siguiente manera:
$$Y_t=\frac{Z_t}{(1-L)^2}=Z_t\times \frac{1}{1-L}\times \frac{1}{1-L} = Z_t\times \left( 1+L+L^2+L^3+\cdots\right )^2$$ $$Y_t = Z_t (1+2L+3L^2+\cdots+(n+1)L^n+\cdots)=Z_t\sum_{i=0}^\infty {(i+1)L^i}$$ $$Y_{T+n}=Y_T+n\times W_T+\sum_{i=1}^{n-1}{(n+1-i)Z_{T+n-i}}$$
For $d=3$, la integración del operador se define así:
$$Y_t=\frac{Z_t}{(1-L)^3}=Z_t\times \frac{1}{1-L}\times \frac{1}{1-L} \times \frac{1}{1-L}= Z_t\times \left( 1+L+L^2+L^3+\cdots\right )^3$$ $$Y_t = Z_t (1+3L+6L^2+\cdots+\frac{(n+1)(n+2)}{2}L^n+\cdots)=Z_t\sum_{i=0}^\infty {\frac{(i+1)(i+2)}{2}L^i}$$ $$Y_{T+n}=Y_T+n\times W_T+\frac{n(n-1)}{2}V_T+\sum_{i=1}^{n-1}{\frac{(n+1-i)(n+2-i)}{2}Z_{T+n-i}}$$ $$W_T=Y_T-Y_{T-1}$$ $$V_T=W_T-W_{T-1}=Y_T-2Y_{T-1}+Y_{T-2}$$
Dado que $\{Y_t\}$ es una serie de tiempo integrada de orden, luego $Z_t$ es una serie de tiempo estacional la cual tiene una representación de ARMA invertible:
$$Y_t=a_t\sum_{k=0}^\infty {\psi_i L^i}\times \sum_{j=0}^\infty L^i\times \sum_{j=0}^\infty L^i\times \cdots \times \sum_{j=0}^\infty L^i = a_t\sum_{k=0}^\infty {\psi_i L^i}\times \sum_{k=0}^\infty {\zeta_i L^i}\\ $$
Podemos calcular la variable condicional en el tiempo T+n dada la información disponible el el tiempo T:
$$\textrm{Var}\left(Y_{T+n}\|Y_T Y_{T-1}\cdots Y_1 \right )=\textrm{Var}\left( a_t\sum_{k=0}^\infty {\psi_i L^i} \sum_{k=0}^\infty {\zeta_i L^i}\right )=\sigma_a^2\times \sum_{i=1}^{n-1}\gamma_i^2$$
Donde:
$$\gamma_i=\sum_{k=0}^i{\zeta_{i-k}\times \psi_k}$$ $$\zeta_o=\psi_o=1$$
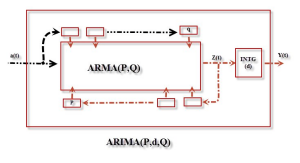
Máquina ARIMA
Tenga en cuenta que estamos observando la salida integrada del proceso ARMA ($Y_t$), Pero la máquina procesa las salidas diferenciadas ($Z_t$). El bloque INTG hace referencia al operador de integración.
¿Cómo sabemos si tenemos una raíz unitaria en nuestra serie de tiempo?
Aparte de las pruebas estadísticas de unidad de raíz (por ejemplo, ADF, KPSS, etc), hay algunas pistas visuales para la detección de raíz unitaria utilizando las gráficas ACF y PACF. Por ejemplo, una serie de tiempo con raíz unitaria exhibirá valores de ACF decaídos altos y muy lentos para todos los retrasos. En el gráfico de PACF, el valor de PACF para el primer retraso es casi uno (1), y los valores de PACF para el orden de retraso mayor que uno son insignificantes./p>
Para las pruebas estadísticas, la prueba de Dickey-Fuller (ADF) aumentada examinará la evidencia de una raíz unitaria, incluso en presencia de una tendencia determinista o una tendencia al cuadrado.
Características Estadísticas
En nuestra descripción del proceso ARIMA, se destacó un solo estímulo de entrada: choques/innovations, enfatizando cómo se propagan a través de la maquinaria ARIMA para generar la producción observada. La máquina ARIMA Excel es básicamente una máquina ARMA, pero la salida está integrada antes de poder observarla. ¿Cómo afecta esto a la distribución de salida?
¿Por Qué Nos Debe Importar?
La distribución estadística (es decir.$\Psi$ ) de la salida ($Y_{T+n}$) Es fundamental para realizar un pronóstico y / o establecer un intervalo de confianza en cualquier momento futuro (T+n).
$$Y_{T+n}\sim \Psi(\mu_{T+n},\sigma_{T+n}^2)$$ $$\mu_{T+n}-Z_{l}^{\alpha/2}\sigma_{T+n}\leqslant \hat Y_{T+n} \leqslant \mu_{T+n}+Z_{u}^{\alpha/2}\sigma_{T+n}$$
Donde:
- $\hat Y_{T+n}$ es el pronóstico de la muestra en el tiempo T+n.
- $Z_{l}^{\alpha/2}$ es el valor crítico más bajo para $\alpha/2$ nivel de significancia.
- $Z_{u}^{\alpha/2}$ es el valor crítico superior para $\alpha/2$ nivel de significancia.
- $\sigma_{T+n}^2$ es la varianza condicional en el tiempo T+n.
Por ahora, la importancia de comprender la distribución estadística de los resultados debe ser clara. Ahora, ¿cómo vamos a formar esa comprensión?
Regresando a la definición, la serie de tiempo diferenciada ${Z_t}$ es modelada como un proceso estacional ARMA.
$$(1-\sum_{i=1}^p{\phi_i L^i})Z_t=(1+\sum_{j=1}^q \theta_j L^j)a_t$$ $$Z_t=\frac{1+\sum_{j=1}^q \theta_j L^j}{1-\sum_{i=1}^p{\phi_i L^i}}=(1+\sum_{i=1}^\infty{\psi_i L^i})a_t=\sum_{i=0}^\infty{\psi_i L^i}a_t$$ $$\psi_o=1$$
Ahora, recuperemos la serie de tiempo original de $\{Z_t\}$.
Ejemplo:
Consideremos las siguientes series diferenciadas $Z_t=(1-L)Y_t$. Para recuperar la serie de tiempo $\{Y_t\}$, Simplemente sumamos todas las diferencias hasta la fecha.
$$Z_T=Y_T-Y_{T-1}$$ $$Y_{T+n}=Y_T+\sum_{i=1}^n{Z_{T+i}}=Y_T+\left( \sum_{i=1}^n\sum_{j=0}^\infty{\psi_j L^j}\right ) a_{T+n}=Y_T+\sum_{i=1}^n\left(a_{T+i}\sum_{j=0}^{i-1}\psi_j \right )$$
Ahora, la varianza del pronóstico se expresa de la siguiente manera:
$$\textrm{Var}\left(Y_{T+n} \right )=\sigma_a^2 \times \sum_{k=1}^n\left(\sum_{i=0}^{n-k} \psi_i \right )^2$$
Como vemos, aunque el cálculo del pronóstico es simple ejercicio de sumar todas las diferencias anteriores, el cálculo de la varianza es mucho más complicado.
Además, como $n\gg 1$, the $Z_{T+n} \to \frac{\mu}{1-\sum_{i=1}^p{\phi_i}}$, entonces la $Y_{T+n}$ estimación/pronóstico asintóticamente se aproxima a la tendencia lineal determinista definida por $Y_T + \frac{n\times \mu}{1-\sum_{i=1}^p{\phi_i}}$.
Conclusión
En términos simples, un proceso ARIMA es simplemente un proceso ARMA cuyas salidas han pasado por un integrador. El integrador hace que las series de tiempo observadas $\{Y_t\}$ sean no estacionarias.El proceso de integración introduce la raíz unitaria en $\{Y_t\}$. La integración de varias veces introduce múltiples raíces unitarias en la serie de tiempo de salida. Esta es la razón por la que la palabra “integrado” se utiliza en ARIMA.
El principal producto de este trabajo es que la diferenciación es un procedimiento especial de transformación que tiene como objetivo convertir una serie de tiempo no estacionaria en una estacionaria. Al igual que todas las transformaciones, se debe tener cuidado al interpretar los resultados de nuevo en el espacio de la serie de tiempo original.
Observe que el modelado de raíz unitaria (por ejemplo, ARIMA) está destinado a capturar una tendencia estocástica y no es adecuado para una tendencia determinista. Si usted sospecha la presencia de una tendencia determinista, debe explorar primero esta avenida (es decir, regresar con el tiempo). En ese punto, puede optar por tomar los residuos y aplicar un proceso de tipo ARMA para explotar cualquier dinámica restante.