Análisis de Componentes Principales (ACP) 101
Esta es la primera entrada en lo que se convertirá en una serie en curso sobre análisis de componentes principales en Excel (ACP). En este tutorial, comenzaremos con la definición general, la motivación y las aplicaciones de un ACP y luego usaremos NumXL para llevar a cabo dicho análisis.A continuación, vamos a examinar de cerca los diferentes elementos de salida en un intento de desarrollar una sólida comprensión del ACP, que preparará el camino a un tratamiento más avanzado en las ediciones futuras.
En este tutorial, usaremos los datos socioeconómicos proporcionados por Harman (1976). Las cinco variables representan población total (“Población”), mediana de años escolares (“Escuela”), empleo total (“Empleo”), servicios profesionales diversos (“Servicios”) y valor promedio de vivienda. Cada observación representa uno de los doce tramos del censo en el área metropolitana estadística de Los Ángeles.
Preparación de Datos
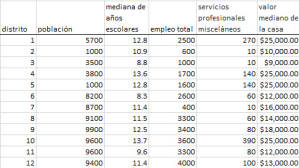
Primero, organicemos nuestros datos de entrada. En primer lugar, colocamos los valores de cada variable en una columna separada, y cada observación (es decir, zona censal en LA) en una fila separada.
Obsérvese que las escalas (es decir, la magnitud) de las variables varían significativamente, de modo que cualquier análisis de datos sin procesar estará sesgado hacia las variables con una escala más grande, y minimizará el efecto de aquellos con una menor escala.
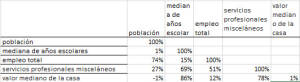
Para entender mejor el problema, calculemos la matriz de correlación para las 5 variables:
Las cinco (5) variables están altamente correlacionadas, por lo que uno puede preguntarse:
- Si fuéramos a utilizar esas variables para predecir otra variable, ¿necesitamos las 5 variables?
- ¿Hay fuerzas ocultas (controladores u otros factores) que mueven esas 5 variables?
En la práctica, a menudo encontramos series de datos correlacionados: los precios de los productos básicos en diferentes lugares, los precios futuros para diferentes contratos, los precios de las acciones, los tipos de interés, etc.
En pocas palabras, ¿qué es el análisis de componentes principales en Excel (ACP)?
ACP es una técnica que toma un conjunto de variables correlacionadas y transforma linealmente esas variables en un conjunto de factores no correlacionados.
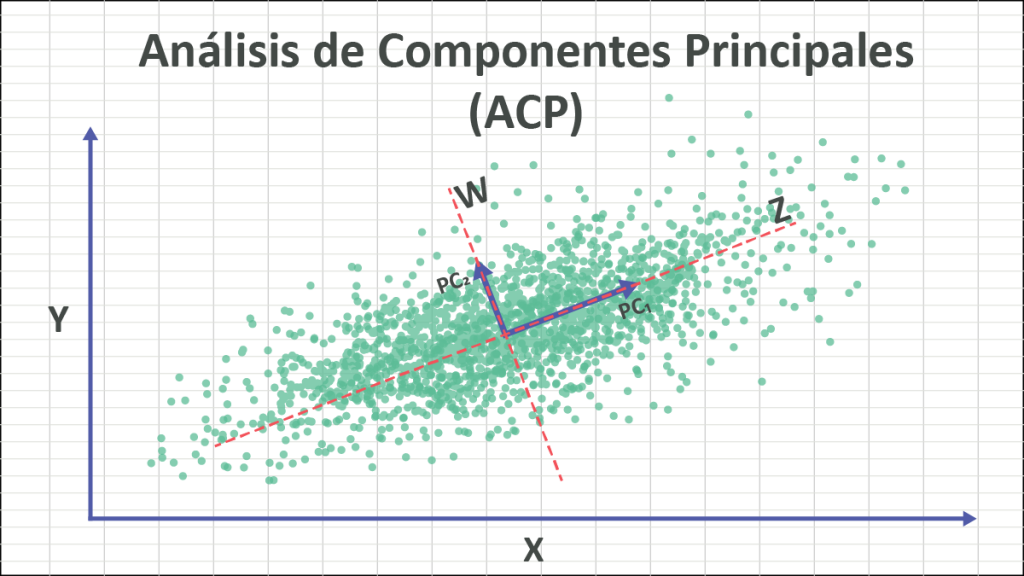
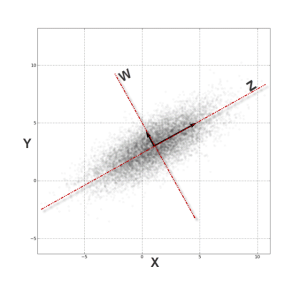
Para explicarlo más a fondo, se puede pensar en el ACP como una transformación del sistema de eje. Examinemos este gráfico de dos variables correlacionadas:
En pocas palabras, a partir del sistema cartesiano (X, Y), los puntos de datos están altamente correlacionados. Mediante la transformación (rotación) del eje en (Z, W), los puntos de datos ya no están correlacionados.
En teoría, el ACP encuentra que esas transformaciones (del eje) de los puntos de datos parecerán no correlacionadas con su estimación.
OK, ahora ¿dónde están los componentes principales?
Para transformar los puntos de datos del sistema cartesiano (X, Y) a (Z, W), necesitamos calcular los valores z y w de cada punto de datos:
$$z_i=\alpha_1 x_i + \beta_1 y_i$$ $$w_i=\alpha_2 x_i + \beta_2 y_i$$
En efecto, estamos reemplazando las variables de entrada ($x_i,y_i$) con los de ($z_i,w_i$). Los valores son aquellos a los que nos referimos como los componentes principales.
Bien, ¿cómo reducimos las dimensiones de las variables?
Cuando transformamos los valores de los puntos de datos ($x_i,y_i$) en el nuevo sistema de ejes ($z_i,w_i$), Podemos encontrar que algunos ejes capturan más de la variación de los valores que otros. Por ejemplo, en nuestro ejemplo anterior,podemos afirmar que todos los valores $w_i$ son cero y realmente no importa.
$$ \left.\begin{matrix} x_i=\gamma_1 z_i + \phi_1 y_i \\\\ y_i=\gamma_2 z_i +
\phi_2 y_i \end{matrix}\right\} \Rightarrow \left.\begin{matrix} x_i=\gamma_1
z_i \\\\ y_i=\gamma_2 z_i \end{matrix}\right\} $$
En efecto, el sistema bidimensional ($z_i,w_i$) se reduce a un sistema unidimensional ($z_i$).
Por supuesto, para este ejemplo, el factor $W$ distorsiona nuestros datos, pero para dimensiones superiores puede no ser tan malo.
¿Qué componente debemos dejar?
En la práctica, se ordenan los componentes (factores) en términos de su varianza (la más alta primero) y se examina el efecto de eliminar los de menor varianza (la derecha más) en un esfuerzo para reducir la dimensión del conjunto de datos con una pérdida mínima de información.
¿Por qué deberíamos preocuparnos por los componentes principales?
Un gerente de riesgos puede cuantificar su riesgo general en términos de una exposición agregada de portafolio a un pequeño grupo de conductores, en lugar de decenas de cientos de precios de valores correlacionados. Además, el diseño de una estrategia de cobertura eficaz se simplifica enormemente.
Para los comerciantes, la cuantificación de las transacciones en términos de sus sensibilidades (por ejemplo, delta, gamma, etc.) a los conductores le da opciones de negociación para sustituir (o negociar) una valor por otro, construir una estrategia comercial, contabilizar, sintetizar un valor, etc.
Un modelador de datos puede reducir el número de variables de entrada con una pérdida mínima de información.
El Proceso
Estamos listos para realizar nuestro análisis de componentes principales en Excel. En primer lugar, seleccione una celda vacía en la hoja de cálculo donde desea que se genere la salida, a continuación, busque y haga clic en el icono “ACP” en la pestaña NumXL (o barra de herramientas).
Aparecerá el Asistente para el análisis de componentes principales.
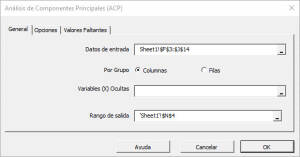
Seleccione el rango de celdas para los cinco valores de las variables de entrada.
- El rango de celdas incluye (opcional) la celda de encabezado ("Etiqueta"), que se utilizaría en las tablas de salida donde hace referencia a esas variables.
- Las variables de entrada (es decir, X) ya están agrupadas por columnas (cada columna representa una variable), por lo que no es necesario cambiarlo.
- Deje el campo "Máscara de Variable" en blanco por ahora. Revisaremos este campo en entradas posteriores.
- De forma predeterminada, el rango de celdas de salida se establece en la celda seleccionada actualmente en la hoja de cálculo.
Finalmente, una vez que seleccionamos el rango de las celdas de datos de entrada (X), las pestañas “Opciones” y “Valores perdidos” están disponibles (habilitadas).
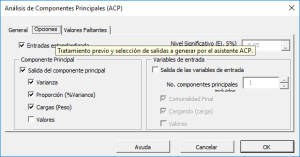
Luego seleccione la pestaña “Opciones”.
- “Estandarizar entrada” está marcada. Esta opción reemplaza en efecto los valores de cada variable por su versión estandarizada (es decir, resta la media y divide por desviación estándar). Esta opción supera el problema de sesgo cuando los valores de las variables de entrada tienen diferentes escalas de magnitud. Deje esta opción marcada.
- Se selecciona “Salida de componente principal”. Esta opción indica al asistente que genere tablas relacionadas con ACP. Dejarlo marcado.
- En “Componente principal”, marque la opción “Valores” para mostrar los valores de cada componente principal.
- El nivel de significación (alpha) se establece en 5%.
- La opción “Variables de entrada” está sin marcar. Deje sin marcar por ahora.
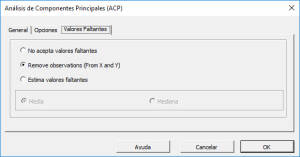
En esta pestaña, puede seleccionar una aproximación para manejar valores faltantes en el conjunto de datos de las (X). Por defecto, cualquier valor faltante encontrado en cualquiera de las variables de entrada (X) en cualquier observación excluiría la observación del análisis.
Este tratamiento es un buen enfoque para nuestro análisis, así que dejémoslo sin cambios.
Ahora, haga clic en “OK” para generar las tablas de resultados.
Análisis
1. Estadísticas ACP
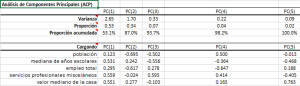
- Los componentes principales se ordenan (y se denominan) de acuerdo con su varianza en un orden descendente, es decir, PC (1) tiene la varianza más alta.
- En la segunda fila, las estadísticas de proporción explican el porcentaje de variación en el conjunto original de datos (5 variables combinadas) que cada componente principal captura o explica.
- La proporción acumulada es una medida de la variación total explicada por los componentes principales hasta este componente actual.
Nota: En nuestro ejemplo, los tres primeros CP representan el 94,3% de la variación de las 5 variables. - Tenga en cuenta que la suma de las varianzas de los CP debe producir el número de variables de entrada, que en este caso es cinco (5).
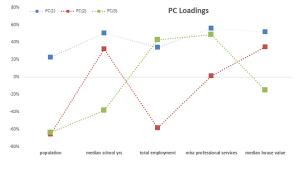
2. Cargas
En la tabla de carga, esbozamos los pesos de una transformación lineal desde el sistema de coordenadas de las variables de entrada (estandarizadas) a los componentes principales.
Por ejemplo, la transformación lineal para $PC_1$ se expresada de la siguiente manera:
$$PC_1=0.27X_1+0.503X_2+0.339X_3+0.56X_4+0.516X_5$$
Nota:
- Las cargas al cuadrado (columna) se suman a una.
$$\sum_{i=1}^5 \beta_i^2 = 1$$
- En el gráfico anterior, trazamos las cargas para nuestras variables de entrada en los tres primeros componentes.
- La mediana de los años escolares, misc. Los servicios profesionales y las medianas de las variables de valor de la casa tienen cargas comparables en PC (1), luego viene la carga total de empleo y finalmente, la población. Uno puede proponer esto como un factor representante del poder de riqueza o ingreso.
- La interpretación de las cargas para las variables de entrada en los componentes restantes resulta ser más difícil y requiere un nivel más profundo de experiencia en el dominio.
- Por último, el cálculo de las variables de entrada desde el PC se puede hacer fácilmente mediante la aplicación de los pesos en la fila en lugar de la columna. Por ejemplo, el factor de población se expresa de la siguiente manera:
$$X_1=0.227 PC_1-0.657PC_2-0.64PC_3+0.308PC_4-0.109PC_5$$ - Discutiremos la carga de la PC más adelante en este tutorial.
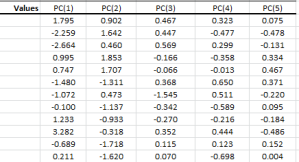
3. Valores de los Componentes Principales
En la tabla de valores del CP, calculamos el valor de salida de transformación para cada dimensión (es decir, componente), por lo que la primera fila corresponde al primer punto de datos, y así sucesivamente.
La varianza de cada columna coincide con el valor de la tabla de estadísticas de la ACP. Utilizando Excel, calcule la versión sesgada de la función de varianza (VARA).
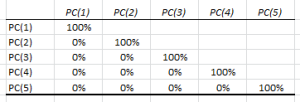
BY, los valores en los CPs no están correlacionados. Para verificar, podemos calcular la matriz de correlación:
Conclusión de ACP
En este tutorial, convertimos un conjunto de cinco variables correlacionadas en cinco variables no correlacionadas sin ninguna pérdida de información.
Además, nosotros examinamos la proporción (y la proporción acumulada) de cada componente como una medida de varianza capturada por cada componente, y se encontró que los tres primeros factores (componentes) representan el 94,3% de la variación de las cinco variables y los cuatro primeros componentes representan el 98%.
Tutorial Video - Análisis de Componentes Principales (ACP)
¿Qué hacemos ahora?
Una de las aplicaciones de ACP es la reducción de la dimensión; podemos dejar uno o más componentes y retener la información en el conjunto de datos original para propósitos de modelado?
En nuestra segunda entrada, veremos la variación de cada variable de entrada capturada por componentes principales (micro-nivel) y calcularemos los valores ajustados usando un conjunto reducido de CPs.
Cubriremos este tema en particular en una entrada independiente de nuestra serie.