Data filtering with Fourier Transform
Process
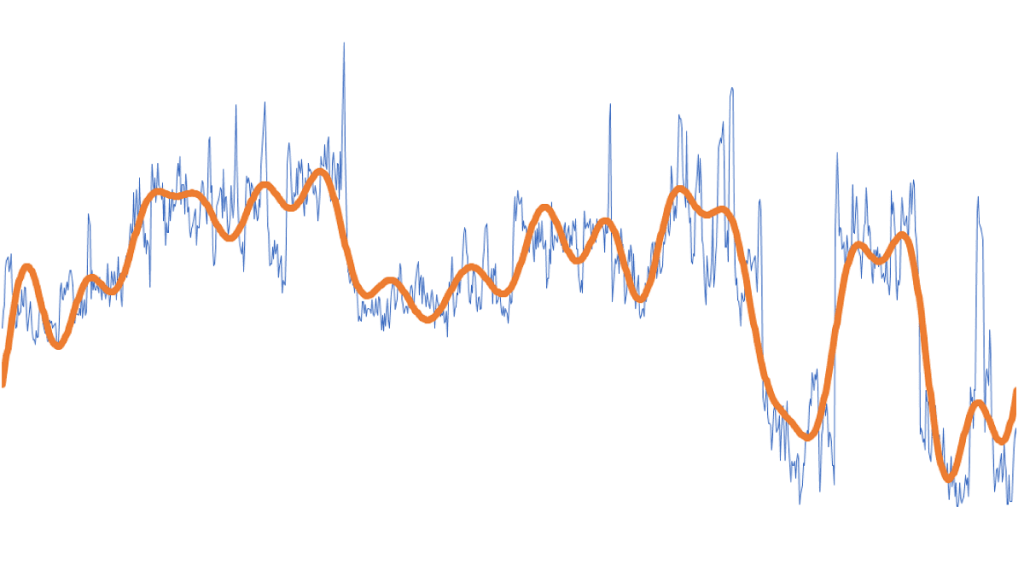
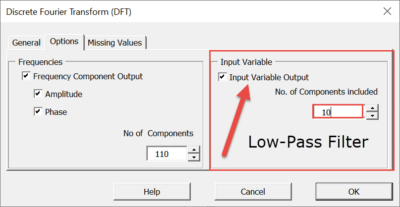
NumXL Discrete Fourier Transform (DFT) wizard supports low-pass filtering by reconstructing the signal using the lower K components, thus removing the higher frequency noise components, and generating a smoother signal.
Unfortunately, we can’t be sure that the first K components are the ones with the highest amplitudes, so we can’t use the wizard for our objective. To proceed with our goal, first, we generate the Fourier spectrum:
Next, we identify the N-components (e.g., N=11) with the highest amplitudes, and derive a new DFT spectrum to include only those components, and set the rest to zero:
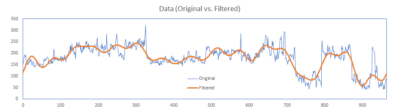
Now, using the modified DFT spectrum and the IDFT function, we can reconstruct
the filtered signal.
Conclusion
In this issue, we have demonstrated a few steps to implement a simple filter in the frequency domain with Fourier transform. You can use this technique, and apply, with little-to-no modification, and build a wide range of more sophisticated filter functions.
Note that we have not touched on the phase part of the Fourier transform, but instead left it unchanged. Shall you wish to implement a filter function that affects the Phase, then you’d account for the change in the Phase and the amplitude of each component in the modified DFT spectrum.
Files Examples
Please click the button below to download the Data Filtering with Fourier Transform example.